2022-2023學(xué)年廣東省梅州市豐順縣潘田第二學(xué)校九年級(jí)（上）月考數(shù)學(xué)試卷（9月份）
發(fā)布：2024/8/23 0:0:1
一、選擇題（共10題，共30分）
-
1．一元二次方程ax2+bx+c=0有一個(gè)根是零的條件是（ ）
組卷：16引用：5難度：0.9 -
2．已知∠AOB=90°，OC是從∠AOB的頂點(diǎn)O引出的一條射線(xiàn)，若∠AOB=2∠BOC，則∠AOC=（ ）
組卷：39引用：2難度：0.7 -
3．某種品牌運(yùn)動(dòng)服經(jīng)過(guò)兩次降價(jià)，每件零售價(jià)由a元降為b元，已知兩次降價(jià)的百分率相同，求每次降價(jià)的百分率設(shè)每次降價(jià)的百分率為x,下面所列的方程中正確的是（ ）
組卷：257引用：3難度：0.6 -
4．如圖，在菱形ABCD中，E，F(xiàn)，G，H分別是菱形四邊的中點(diǎn)，連接EG與FH交于點(diǎn)O，則圖中共有菱形（ ）組卷：749引用：17難度：0.7 -
5．如圖，在菱形ABCD中，M，N分別在AB，CD上，且AM=CN，MN與AC交于點(diǎn)O，連接BO．若∠DAC=28°，則∠OBC的度數(shù)為（ ）組卷：10012引用：119難度：0.7 -
6．如圖，在一張矩形紙片ABCD中，AB=4，BC=8，點(diǎn)E，F(xiàn)分別在AD，BC上，將紙片ABCD沿直線(xiàn)EF折疊，點(diǎn)C落在AD上的一點(diǎn)H處，點(diǎn)D落在點(diǎn)G處，有以下四個(gè)結(jié)論：
①四邊形CFHE是菱形；
②EC平分∠DCH；
③線(xiàn)段BF的取值范圍為3≤BF≤4；
④當(dāng)點(diǎn)H與點(diǎn)A重合時(shí)，EF=2．5
以上結(jié)論中，你認(rèn)為正確的有（ ）個(gè)．組卷：2623引用：66難度：0.5 -
7．如圖，矩形ABCD的對(duì)角線(xiàn)相交于點(diǎn)O，OF⊥AB，BE⊥AC，E是OC的中點(diǎn)，OF=4，則BD的長(zhǎng)為（ ）組卷：1012引用：3難度：0.4 -
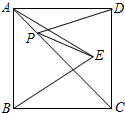8．如圖，正方形ABCD的面積為4，△ABE是等邊三角形，點(diǎn)E在正方形ABCD內(nèi)，在對(duì)角線(xiàn)AC上有一點(diǎn)P，使PD+PE的和最小，則這個(gè)最小值為（ ）組卷：2247引用：13難度：0.9
三、解答題（共8題，共62分）
-
24．如圖，正方形ABCD中，AB=6，點(diǎn)E在邊CD上，且CD=3DE，將△ADE沿AE對(duì)折至△AFE，延長(zhǎng)EF交邊BC于點(diǎn)G，連接AG、CF．
（1）求證：△ABG≌△AFG；
（2）求BG的長(zhǎng)；
（3）求△FEC的面積．組卷：301引用：2難度：0.1 -
25．如圖1，點(diǎn)O是正方形ABCD兩對(duì)角線(xiàn)的交點(diǎn)，分別延長(zhǎng)OD到點(diǎn)G，OC到點(diǎn)E，使OG=2OD，OE=2OC，然后以O(shè)G、OE為鄰邊作正方形OEFG，連接AG，DE．
（1）求證：DE⊥AG；
（2）正方形ABCD固定，將正方形OEFG繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)α角（0°＜α＜360°）得到正方形OE′F′G′，如圖2．
①在旋轉(zhuǎn)過(guò)程中，當(dāng)∠OAG′是直角時(shí)，求α的度數(shù)；
②若正方形ABCD的邊長(zhǎng)為1，在旋轉(zhuǎn)過(guò)程中，求AF′長(zhǎng)的最大值和此時(shí)α的度數(shù)，直接寫(xiě)出結(jié)果不必說(shuō)明理由．
組卷：5670引用：33難度：0.5