2021-2022學年上海市黃浦區大同中學高三（下）開學數學試卷

一、填空題

• 1．行列式

  1	2 i
  i	3

  的值等于

  ．
  組卷：10引用：1難度：0.9

  解析

• 2．已知復數z滿足z（2+i）=5（i為虛數單位），則z的值為

  ．
  組卷：45引用：1難度：0.8

  解析

• 3．

  lim

  n

  →∞

  3

  n

  +

  2

  n

  3

  n

  +

  2

  n

  +

  3

  =

  ．
  組卷：63引用：1難度：0.7

  解析

• 4．向量

  a

  、

  b

  滿足|

  a

  +

  b

  |=

  11

  ，|

  a

  -

  b

  |=

  3

  ，則

  a

  ?

  b

  =

  ．
  組卷：148引用：3難度：0.5

  解析

• 5．若等差數列{a_n}前n項和為S_n，a₂+a₄=14，S₇=70，則{a_n}的通項公式為a_n=

  ．
  組卷：155引用：2難度：0.8

  解析

• 6．在（x+

  1

  x

  ）⁶的二項展開式中，常數項是

  （用數字作答）．
  組卷：39引用：3難度：0.8

  解析

• 7．直線l：

  x = 2 + 2 t

  y = - 1 - t

  （t是參數）的傾斜角為

  ．
  組卷：38引用：1難度：0.8

  解析

三、解答題

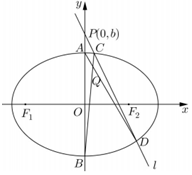• 20．在平面直角坐標系中，A、B分別為橢圓Γ：

  x

  2

  2

  +

  y

  2

  =

  1

  的上、下頂點，若動直線l過點P（0，b）（b＞1），且與橢圓Γ相交于C、D兩個不同點（直線l與y軸不重合，且C、D兩點在y軸右側，C在D的上方），直線AD與BC相交于點Q．
  （1）設Γ的兩焦點為F₁、F₂，求∠F₁AF₂的值；
  （2）若b=3，且

  PD

  =

  3

  2

  PC

  ，求點Q的橫坐標；
  （3）是否存在這樣的點P，使得點Q的縱坐標恒為

  1

  3

  ？若存在，求出點P的坐標，若不存在，請說明理由．
  組卷：227引用：3難度：0.6

  解析

• 21．已知在每一項均不為0的數列{a_n}中，a₁=3，且

  a

  n

  +

  1

  =

  p

  a

  n

  +

  t

  a

  n

  （p,t為常數，n∈N^*），記數列{a_n}的前n項和為S_n．
  （1）當t=0時，求S_n；
  （2）當p=

  1

  2

  ，t=2時，
  ①求證：數列

  {

  lg

  a

  n

  +

  2

  a

  n

  -

  2

  }

  為等比數列；
  ②是否存在正整數m,使得不等式S_n-2n＜m對任意n∈N^*恒成立？若存在，求出m的最小值；若不存在，請說明理由．
  組卷：216引用：4難度：0.3

  解析