2022-2023學年上海市徐匯區位育中學高二（上）月考數學試卷（10月份）

一、填空題（本大題共有12題，滿分54分）

• 1．平面的一條斜線和這個平面所成角θ的取值范圍是

  ．
  組卷：90引用：4難度：0.7

  解析

• 2．設∠A與∠B的兩邊分別平行，若∠A=45°，則∠B的大小為

  ．
  組卷：324引用：6難度：0.9

  解析

• 3．從同一點出發的四條直線最多能確定

  個平面．
  組卷：216引用：6難度：0.8

  解析

• 4．下列判斷中：①三點確定一個平面；②一條直線和一點確定一個平面；③兩條直線確定一個平面；④三角形和梯形一定是平面圖形；⑤四邊形一定是平面圖形；⑥六邊形一定是平面圖形；⑦兩兩相交的三條直線確定一個平面．其中正確的是

  ．
  組卷：517引用：6難度：0.7

  解析

• 5．設a,b是平面M外兩條直線，且a∥M，那么a∥b是b∥M的

  條件．
  組卷：96引用：4難度：0.9

  解析

• 6．若用“斜二測法”作出邊長為2的正三角形△ABC的直觀圖是△A₁B₁C₁，則△A₁B₁C₁的重心G₁到底邊A₁B₁的距離是

  ．
  組卷：72引用：3難度：0.7

  解析

• 7．已知直線a、b是正方體上兩條面對角線所在的直線，且a、b是異面直線，則直線a、b所成的角的大小為

  ．
  組卷：34引用：2難度：0.7

  解析

三、解答題（本大題共有5題，滿分76分）

• 20．已知四面體P-ABC（如圖1）的平面展開圖（如圖2）中，四邊形ABCD為邊長為

  2

  的正方形，△ABE和△BCF均為正三角形，在四面體P-ABC中：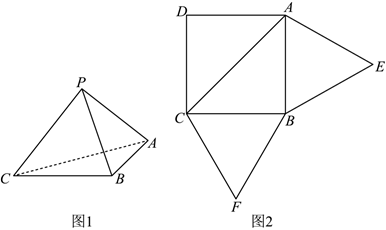
  
  （1）證明：平面PAC⊥平面ABC；
  （2）求二面角A-PC-B的余弦值；
  （3）在圖1中作出直線CA與平面ABP的所成角，并求出直線CA與平面ABP的所成角的大小．
  組卷：74引用：2難度：0.5

  解析

• 21．空間中的距離有多種，包括兩點間距離、點到直線距離、點到平面距離、直線到平面距離、兩平行平面中的距離等，其中兩條異面直線的距離指的是公垂線（與兩條異面直線都垂直相交的直線）的兩個垂足之間的線段長度．
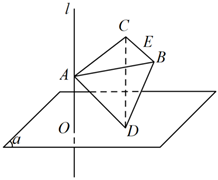
  如圖，直線l⊥平面α，垂足為O，正四面體ABCD的所有棱長都為2，A，D分別是直線l和平面α上的動點，且BC⊥l.
  （1）點O到棱BC中點E的距離的最大值為

  ；
  （2）正四面體ABCD在平面α上的射影面積的最大值為

  ．
  組卷：68引用：2難度：0.5

  解析