2023年北京大學附中高考數學三模試卷

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.

• 1．已知集合P={x|x²≤4}，M={m}，若P∩M=M，則m的取值范圍是（　　）

  A．（-∞，-2]	B．[-2，2]
  C．[2，+∞）	D．（-∞，-2]∪[2，+∞）
  組卷：631引用：5難度：0.7

  解析

• 2．拋物線y²=8x的焦點到準線的距離是（　　）

  A．1

  B．2

  C．4

  D．8
  組卷：645引用：57難度：0.9

  解析

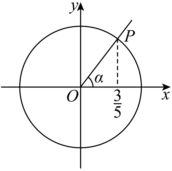• 3．如圖，點P為角α的終邊與單位圓O的交點，tan（α+π）=（　　）

  A． - 3 4

  B． 3 4

  C． - 4 3

  D． 4 3
  組卷：269引用：3難度：0.7

  解析

• 4．在

  （

  x

  +

  2

  x

  ）

  3

  的展開式中，常數項為（　　）

  A．1

  B．3

  C．6

  D．12
  組卷：136引用：2難度：0.7

  解析

• 5．現從3名男同學和2名女同學中選取兩人加入“數學興趣小組”，用A表示事件“抽到兩名同學性別相同”，B表示事件“抽到兩名女同學”，則在已知A事件發生的情況下B事件發生的概率即P（B|A）=（　　）

  A． 1 4

  B． 1 3

  C． 2 5

  D． 1 2
  組卷：572引用：7難度：0.7

  解析

• 6．已知圓O：x²+y²=1，直線3x+4y-10=0上動點P，過點P作圓O的一條切線，切點為A，則|PA|的最小值為（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：1190引用：11難度：0.8

  解析

• 7．將函數y=sin2x的圖象向左平移φ（φ＞0）個單位，得到的圖象恰好關于直線x=

  π

  6

  對稱，則φ的最小值是（　　）

  A． π 12

  B． π 6

  C． π 4

  D． π 3
  組卷：411引用：6難度：0.7

  解析

三、解答題共6題，共85分.解答應寫出文字說明、演算步驟或證明過程.

• 20．已知函數f（x）=e^ax（x-1）²．
  （1）若a=1，求f（x）在（0，f（0））處切線方程；
  （2）求f（x）的極大值與極小值；
  （3）證明：存在實數M，當a＞0時，函數y=f（x）-M有三個零點．
  組卷：449引用：7難度：0.5

  解析

• 21．已知A為有限個實數構成的非空集合，設A+A={a_i+a_j|a_i，a_j∈A}，A-A={a_i-a_j|a_i，a_j∈A}，記集合A+A和A-A其元素個數分別為|A+A|，|A-A|．
  設n（A）=|A+A|-|A-A|．例如當A={1，2}時，A+A={2，3，4}，A-A={-1，0，1}，|A+A|=|A-A|，所以n（A）=0．
  （1）若A={1，3，5}，求n（A）的值；
  （2）設A是由3個正實數組成的集合且（A+A）∩A=?，A′=A∪{0}，證明：n（A′）-n（A）為定值；
  （3）若{a_n}是一個各項互不相同的無窮遞增正整數數列，對任意n∈N^*，設A_n={a₁，a₂，…，a_n}，b_n=n（A_n）．已知a₁=1，a₂=2，且對任意n∈N^*，b_n≥0，求數列{a_n}的通項公式．
  組卷：233引用：5難度：0.3

  解析