2023年貴州省畢節市高考數學診斷試卷（文科）（二）

一、選擇題：本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知全集U=R，集合A={x|-5＜x≤3}，B={x|1＜x＜4}，則（?_UA）∪B=（　　）

  A．{x|x≤-5或x＞1}

  B．{x|x≤-5或x＞3}

  C．{x|1＜x＜4}

  D．{x|1＜x≤3}
  組卷：187引用：6難度：0.8

  解析

• 2．已知復數

  z

  =

  2

  i

  1

  +

  i

  3

  +

  1

  ，則|z|=（　　）

  A． 2 + 1

  B． 2

  C．1

  D． 5
  組卷：75引用：3難度：0.8

  解析

• 3．已知a,b為兩條不同的直線，α，β為兩個不同的平面，則下列命題中正確的是（　　）

  A．若a∥b,b∥α，則a∥α	B．若a∥b,a⊥α，b∥β，則α⊥β
  C．若a∥α，b∥β，α∥β，則a∥b	D．若a∥α，b∥β，α⊥β，則a⊥b
  組卷：280引用：5難度：0.6

  解析

• 4．古希臘數學家阿波羅尼斯在《圓錐曲線論》中，記載了用平面截圓錐得到圓錐曲線的辦法．如圖，已知圓錐的高與底面半徑均為2，過軸OO₁的截面為平面OAB，平行于平面OAB的平面α與圓錐側面的交線為雙曲線C的一部分．若雙曲線C的兩條漸近線分別平行于OA，OB，則建立恰當的坐標系后，雙曲線C的方程可以為（　　）

  A． y 2 - x 2 4 = 1

  B． y 2 4 - x 2 = 1

  C．y2-x2=1

  D． y 2 2 - x 2 = 1
  組卷：97引用：5難度：0.5

  解析

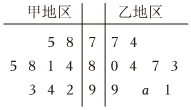• 5．某市質量檢測部門從轄區內甲、乙兩個地區的食品生產企業中分別隨機抽取9家企業，根據食品安全管理考核指標對抽到的企業進行考核，并將各企業考核得分整理成如下的莖葉圖．由莖葉圖所給信息，可判斷以下結論中正確是（　　）

  A．若a=2，則甲地區考核得分的極差大于乙地區考核得分的極差

  B．若a=4，則甲地區考核得分的平均數小于乙地區考核得分的平均數

  C．若a=5，則甲地區考核得分的方差小于乙地區考核得分的方差

  D．若a=6，則甲地區考核得分的中位數小于乙地區考核得分的中位數
  組卷：52引用：4難度：0.7

  解析

• 6．將函數y=sin2x的圖象向左平移

  π

  6

  個單位長度，所得圖象的對稱軸中與y軸距離最近的是（　　）

  A． x = - π 12

  B． x = - π 6

  C． x = π 6

  D． x = π 12
  組卷：84引用：3難度：0.7

  解析

• 7．有詩云：“芍藥承春寵，何曾羨牡丹”，芍藥不僅觀賞性強，且具有藥用價值，某地以芍藥為主打造了一個如圖的花海大世界，其中大圓半徑為8，大圓內部的同心小圓半徑為3，兩圓之間的圖案是對稱的．若在其中陰影部分種植紅芍．倘若你置身此花海大世界之中，則恰好處在紅芍中的概率是（　　）

  A． 1 2

  B． 21 50

  C． 55 128

  D． 55 64
  組卷：46引用：3難度：0.8

  解析

請考生在第22、23題中任選一題作答，如果多做，則按所做的第一題記分．作答時用2B鉛筆在答題卡上把所選題目對應題號的方框涂黑．（本題滿分10分）[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系xOy中，以坐標原點O為極點，x軸的正半軸為極軸建立極坐標系．已知曲線C₁的參數方程為

  x = 2 cosθ

  y = sinθ

  （θ為參數），曲線C₂的參數方程為

  x = 2 + tcosα

  y = tsinα

  （t為參數，0＜α＜π）．
  （1）求曲線C₁的極坐標方程與曲線C₂的普通方程；
  （2）點P（2，0），若曲線C₁與曲線C₂有且只有一個交點M，求|PM|的值．
  組卷：34引用：3難度：0.6

  解析

[選修4-5：不等式選講]（本題滿分0分）

• 23．已知a,b,c都是正數，且a+b+c=1．證明：
  （1）

  abc

  ≤

  1

  27

  ；
  （2）

  a

  b

  +

  c

  +

  b

  a

  +

  c

  +

  c

  a

  +

  b

  ≤

  1

  2

  abc

  ．
  組卷：27引用：3難度：0.6

  解析