2023-2024學年寧夏銀川二中高二（上）期中數學試卷

一、選擇題：本大題共8小題，每小題5分，共40分（在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．在正方體ABCD-A₁B₁C₁D₁中，

  BC

  -

  DC

  +

  AB

  =（　　）

  A． BD

  B． DB

  C． AD

  D． DA
  組卷：170引用：6難度：0.7

  解析

• 2．如果拋物線y²=ax的準線是直線x=2，那么它的焦點坐標為（　　）

  A．（2，0）

  B．（1，0）

  C．（-1，0）

  D．（-2，0）
  組卷：76引用：2難度：0.7

  解析

• 3．“a=2”是“直線l₁：2ax+4y+3=0與直線l₂：x-（a-1）y-5=0垂直”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：45引用：4難度：0.7

  解析

• 4．若方程

  x

  2

  2

  +

  m

  -

  y

  2

  2

  -

  m

  =

  1

  表示雙曲線，則m的取值范圍是（　　）

  A．-2＜m＜2

  B．m＞-2

  C．m≥0

  D．m≥2
  組卷：313引用：9難度：0.8

  解析

• 5．古希臘數學家阿波羅尼奧斯（約公元前262～公元前190年）的著作（圓錐曲線論）是古代世界的科學成果，著作中有這樣一個命題：平面內與兩個定點距離之比為常數k（k＞0且k≠1）的點的軌跡為圓．后人將這個圓稱為阿波羅尼斯圓．已知O（0，0），A（3，0）．動點P（x,y）滿足

  |

  PA

  |

  |

  PO

  |

  =

  2

  ，則動點P的軌跡與圓（x-2）²+y²=2的位置關系是（　　）

  A．內含

  B．相離

  C．內切

  D．相交
  組卷：53引用：3難度：0.7

  解析

• 6．已知P，A，B，C是球O面上的四個點，PA⊥面ABC，PA=a,

  AB

  ?

  AC

  =0，

  BC

  =

  2

  PA

  ，則該球體的體積為（　　）

  A． 3 2 a 3 π

  B． 3 2 a 3 π

  C． 3 4 a 3 π

  D． 6 a 3 π
  組卷：61引用：3難度：0.6

  解析

• 7．已知P為拋物線E：y²=2px（p＞0）上一動點，F為E的焦點，點Q為圓x²-4x+y²+3=0上一動點，若|PF|+|PQ|的最小值為3，則p=（　　）

  A．5

  B．4

  C．3

  D．2
  組卷：85引用：3難度：0.6

  解析

四、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的焦距為2

  3

  ，且過點

  （

  3

  ，

  1

  2

  ）

  ．
  （1）求橢圓方程；
  （2）設直線l：y=kx+m（k≠0）交橢圓C于A，B兩點，且線段AB的中點M在直線x=

  1

  2

  上，求證：線段AB的中垂線恒過定點N．
  組卷：176引用：2難度：0.3

  解析

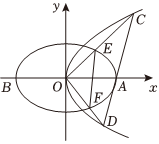• 22．如圖，O為坐標原點，拋物線C₁：y²=2px（p＞0）的焦點是橢圓C₂：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的右焦點，A為橢圓C₂的右頂點，橢圓C₂的長軸AB=8，離心率e=

  1

  2

  ．
  （1）求拋物線C₁橢圓C₂的方程；
  （2）過A點作直線l交C₁于C，D兩點，射線OC，OD分別交C₂于E，F兩點，記△OEF和△OCD的面積分別為S₁和S₂，問是否存在直線l,使得S₁：S₂=3：13？若存在，求出直線l的方程；若不存在，請說明理由．
  組卷：260引用：4難度：0.7

  解析