2022-2023學年廣東省梅州市大埔縣虎山中學高三（上）第三次質檢數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.每小題中，只有一項是符合題目要求的.

• 1．已知集合A={x|2＜x＜5}，B={x|log₃x＞1}，則A∩B=（　　）

  A．（1，3）

  B．（2，5）

  C．（3，5）

  D．（1，5）
  組卷：1引用：2難度：0.7

  解析

• 2．若復數z滿足（1-i）z=3+4i,則|z|=（　　）

  A． 5 2

  B． 5 2 2

  C． 2

  D．5
  組卷：155引用：6難度：0.9

  解析

• 3．若函數

  y

  =

  （

  m

  2

  -

  3

  m

  +

  3

  ）

  x

  m

  2

  +

  2

  m

  -

  4

  為冪函數，且在（0，+∞）單調遞減，則實數m的值為（　　）

  A．0

  B．1或2

  C．1

  D．2
  組卷：1011引用：11難度：0.8

  解析

• 4．古代將圓臺稱為“圓亭”，《九章算術》中“今有圓亭，下周三丈，上周二丈，高一丈，問積幾何？”即一圓臺形建筑物，下底周長3丈，上底周長2丈，高1丈，則它的體積為（　　）

  A． 19 8 π 立方丈	B． 19 12 π 立方丈
  C． 19 π 8 立方丈	D． 19 π 12 立方丈
  組卷：302引用：11難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  e

  |

  x

  |

  x

  -

  x

  的圖象大致為（　　）

  A．

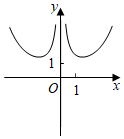
  B．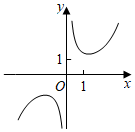

  C．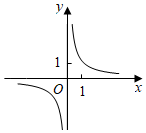

  D．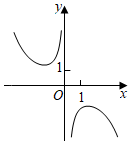
  組卷：323引用：13難度：0.9

  解析

• 6．設a＞0，b＞0．若

  3

  是3^a與3^b的等比中項，則

  1

  a

  +

  3

  b

  的最小值為（　　）

  A． 4 3

  B． 4 + 3

  C． 4 + 2 3

  D．8
  組卷：882引用：5難度：0.5

  解析

• 7．已知直三棱柱ABC-A₁B₁C₁的各頂點都在同一球面上，且該棱柱的體積為

  3

  ，AB=2，AC=1，∠BAC=60°，則該球的表面積為（　　）

  A．4π

  B．4 2 π

  C．8π

  D．32π
  組卷：376引用：11難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．已知函數

  f

  （

  x

  ）

  =

  lnx

  -

  2

  x

  -

  2

  x

  +

  1

  ．
  （1）判斷函數f（x）的零點個數；
  （2）設

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  -

  4

  +

  a

  x

  +

  1

  +

  2

  （

  a

  ∈

  R

  ）

  ，若x₁，x₂是函數g（x）的兩個極值點，求實數a的取值范圍．
  組卷：49引用：3難度：0.5

  解析

• 22．已知函數f（x）=

  1

  4

  x³-x²+x.
  （Ⅰ）求曲線y=f（x）的斜率為1的切線方程；
  （Ⅱ）當x∈[-2，4]時，求證：x-6≤f（x）≤x；
  （Ⅲ）設F（x）=|f（x）-（x+a）|（a∈R），記F（x）在區間[-2，4]上的最大值為M（a）．當M（a）最小時，求a的值．
  組卷：4461引用：9難度：0.5

  解析