2022-2023學年陜西省西安市雁塔二中七年級（下）第一次月考數學試卷

一、選擇題（每小題3分，共30分）

• 1．計算（-3x³y）²正確的是（　　）

  A．6x6y2

  B．9x5y2

  C．9x6y2

  D．-3x3y2
  組卷：319引用：3難度：0.7

  解析

• 2．新型冠狀病毒屬于β屬的新型冠狀病毒，有包膜，顆粒呈圓形或者橢圓形，常為多形性，一個病毒的直徑約為0.00000014m,用科學記數法可表示為（　　）

  A．0.14×10-6m

  B．1.4×10-6m

  C．1.4×10-7m

  D．1.4×10-8m
  組卷：212引用：6難度：0.8

  解析

• 3．已知α與β互為余角，若α=20°，則β的補角的大小為（　　）

  A．70°

  B．110°

  C．140°

  D．160°
  組卷：305引用：5難度：0.7

  解析

• 4．下列各式中，不能用平方差公式計算的是（　　）

  A．（-x-y）（x-y）	B．（-x+y）（-x-y）
  C．（x+y）（-x+y）	D．（x-y）（-x+y）
  組卷：2545引用：115難度：0.9

  解析

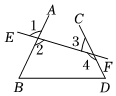• 5．如圖，下列說法正確的是（　　）

  A．∠1和∠B是同位角	B．∠2和∠3是內錯角
  C．∠3和∠4是對頂角	D．∠B和∠4是同旁內角
  組卷：3395引用：8難度：0.7

  解析

• 6．若a^m=2，aⁿ=5，則a^m+n等于（　　）

  A．7

  B．10

  C．25

  D．32
  組卷：1338引用：6難度：0.8

  解析

• 7．若二次三項式4x²+mxy+9y²是一個完全平方式，則m的可能值是（　　）

  A．±6

  B．12

  C．6

  D．±12
  組卷：1183引用：10難度：0.8

  解析

三、解答題（共7小題，共55分，解答應寫出過程）

• 21．當我們利用兩種不同的方法計算同一圖形的面積時，可以得到一個等式，例如，由圖1，可得等式：（a+2b）（a+b）=a²+3ab+2b²．
  
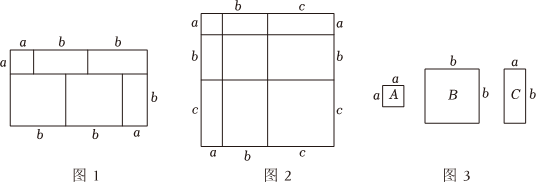
  （1）由圖2，可得等式：

  ．
  （2）利用（1）中所得到的結論，解決下面的問題：已知a+b+c=12，ab+bc+ac=28，求a²+b²+c²的值．
  組卷：698引用：4難度：0.5

  解析

• 22．仔細閱讀材料，再嘗試解決問題：
  完全平方式x²±2xy+y²=（x±y）²以及（x±y）²的值為非負數的特點在數學學習中有廣泛的應用，比如探求x²+6x+10的最大（小）值時，我們可以這樣處理：
  例如：用配方法解題如下：x²+6x+10
  原式=x²+6x+9+1=（x+3）²+1
  因為無論x取什么數，都有（x+3）²的值為非負數，所以（x+3）²的最小值為0；此時x=-3時，進而（x+3）²+1的最小值是0+1=1；所以當x=-3時，原多項式的最小值是1．
  請根據上面的解題思路，探求：
  （1）若（x-5）²=0，則x=

  ．
  （2）已知x²+y²+2x-6y+10=0，求x+y的值．
  （3）已知多項式A為5x²+4y²+4xy-12x,問當x,y分別取何值時A有最小值？并求出A的最小值．
  組卷：611引用：4難度：0.6

  解析