2020-2021學年山東省泰安市泰山英才學校高一（下）期末數學考前模擬練習試卷

一、選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若復數z₁對應復平面內的點（2，3），且z₁?z₂=1+i,則復數z₂的虛部為（　　）

  A． - 5 13

  B． 5 13

  C． - 1 13

  D． 1 13
  組卷：49引用：4難度：0.8

  解析

• 2．某網站舉行購物抽獎活動，規定購物消費每滿100元就送一次抽獎機會，中獎的概率為10%．那么以下理解正確的是（　　）

  A．某人抽獎100次，一定能中獎10次

  B．某人消費1000元，至少能中獎1次

  C．某人抽獎1次，一定不能中獎

  D．某人抽獎10次，可能1次也沒中獎
  組卷：199引用：6難度：0.8

  解析

• 3．在△ABC中，若AC=4，AB=6，

  BC

  =

  2

  7

  ，則∠A=（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  組卷：359引用：2難度：0.7

  解析

• 4．已知向量

  a

  =（cos75°，sin75°），

  b

  =（cos15°，sin15°），則|

  a

  -

  b

  |的值為（　　）

  A． 1 2

  B．1

  C．2

  D．3
  組卷：86引用：4難度：0.7

  解析

• 5．演講比賽共有9位評委分別給出某選手的原始評分，評定該選手的成績時，從9個原始評分中去掉1個最高分、1個最低分，得到7個有效評分．7個有效評分與9個原始評分相比，不變的數字特征是（　　）

  A．中位數

  B．平均數

  C．方差

  D．極差
  組卷：5941引用：64難度：0.8

  解析

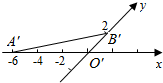• 6．如圖，△O′A′B′是水平放置的△OAB的直觀圖，則△OAB的面積是（　　）

  A．6

  B．3 2

  C．6 2

  D．12
  組卷：671引用：18難度：0.9

  解析

• 7．現采用隨機模擬的方法估計某運動員射擊4次，至少擊中3次的概率：先由計算器給出0到9之間取整數值的隨機數，指定0，1表示沒有擊中目標，2，3，4，5，6，7，8，9表示擊中目標，以4個隨機數為一組，代表射擊4次的結果，經隨機模擬產生了20組隨機數：
  7527?0293?7140?9857?0347?4373?8636?6947?1417?4698
  0371?6233?2616?8045?6011?3661?9597?7424?7610?4281
  根據以上數據估計該射擊運動員射擊4次至少擊中3次的概率為（　　）

  A．0.852

  B．0.8192

  C．0.8

  D．0.75
  組卷：171引用：2難度：0.9

  解析

四、解答題

• 21．11分制乒乓球比賽，每贏一球得1分，當某局打成10：10平后，每球交換發球權，先多得2分的一方獲勝，該局比賽結束．甲、乙兩位同學進行單打比賽，假設甲發球時甲得分的概率為0.5，乙發球時甲得分的概率為0.4，各球的結果相互獨立．在某局雙方10：10平后，甲先發球，兩人又打了X個球該局比賽結束．
  （1）求P（X=2）；
  （2）求事件“X=4且甲獲勝”的概率．
  組卷：9121引用：16難度：0.6

  解析

• 22．如圖，在矩形ABCD中，AB=2AD，M為CD的中點．將△ADM沿AM折起，使得平面ADM⊥平面ABCM．點O是線段AM的中點．
  
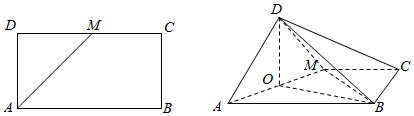
  （Ⅰ）求證：平面DOB⊥平面ABCM；
  （Ⅱ）求證：AD⊥BM；
  （Ⅲ）過D點是否存在一條直線l,同時滿足以下兩個條件：
  ①l?平面BCD；②l∥AM．請說明理由．
  組卷：406引用：5難度：0.5

  解析