2023年河南省平頂山市葉縣高級中學(xué)等高考數(shù)學(xué)模擬試卷（理科）（2月份）（一）

一、選擇題：本大題共12小題，每小題5分，共60分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．若復(fù)數(shù)z滿足（z-i）（z+2i）=0，則z²=（　　）

  A．-1

  B．-4

  C．-1或4

  D．-1或-4
  組卷：61引用：2難度：0.8

  解析

• 2．已知集合A={x|0＜x²＜16}，B={y|2y≥4}，則A∪B=（　　）

  A．?	B．（-4，+∞）
  C．[2，4）	D．（-4，0）∪（0，+∞）
  組卷：33引用：2難度：0.7

  解析

• 3．已知函數(shù)f（x）=ax⁵+bsinx-c,若f（-8）+f（8）=2，則c=（　　）

  A．-1

  B．0

  C．1

  D． 2 3
  組卷：193引用：2難度：0.8

  解析

• 4．已知雙曲線

  C

  ：

  x

  2

  m

  2

  -

  y

  2

  3

  m

  2

  =

  -

  1

  （

  m

  ＞

  0

  ）

  ，則C的離心率為（　　）

  A． 2

  B． 2 3 3

  C． 3

  D．2
  組卷：34引用：1難度：0.7

  解析

• 5．2018年1～10月某市星級酒店經(jīng)營數(shù)據(jù)統(tǒng)計(jì)分析如圖（“同比”指與去年同期相比）：
  
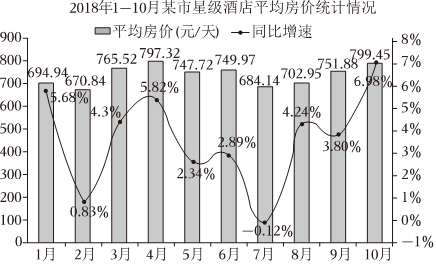
  下列說法錯(cuò)誤的是（　　）

  A．整體來看，2018年1～10月該市星級酒店平均房價(jià)相對上一年有所提高

  B．2018年1～10月該市星級酒店平均房價(jià)的平均數(shù)據(jù)超過700元

  C．2018年1～10月這10個(gè)月中，該市星級酒店在10月份的平均房價(jià)創(chuàng)下10個(gè)月來的最高紀(jì)錄

  D．2017年5月該市星級酒店平均房價(jià)約為720.65元
  組卷：31引用：2難度：0.7

  解析

• 6．已知{a_n}，{b_n}均為等差數(shù)列，且a₃=6，b₁=0，b₂=1，則數(shù)列{a_n+b_n}的前5項(xiàng)和為（　　）

  A．35

  B．40

  C．45

  D．50
  組卷：188引用：4難度：0.7

  解析

• 7．若

  sin

  （

  α

  +

  π

  4

  ）

  =

  -

  3

  5

  ，

  17

  π

  12

  ＜

  α

  ＜

  7

  π

  4

  ，則sin2α+sin²α=（　　）

  A． 16 25

  B． 4 5

  C． 37 50

  D． 7 10
  組卷：156引用：2難度：0.6

  解析

[選修4—4：坐標(biāo)系與參數(shù)方程]

• 22．在平面直角坐標(biāo)系xOy中，曲線C的參數(shù)方程為

  x = 2 + 3 cosα

  y = 3 sinα

  （α為參數(shù)），以坐標(biāo)原點(diǎn)O為極點(diǎn)，x軸的非負(fù)半軸為極軸建立極坐標(biāo)系，直線l的極坐標(biāo)方程是2ρcosθ-ρsinθ-1=0．
  （1）求曲線C的普通方程和直線l的直角坐標(biāo)方程；
  （2）若直線l與曲線C交于A，B兩點(diǎn)，點(diǎn)P（0，-1），求

  1

  |

  PA

  |

  +

  1

  |

  PB

  |

  的值．
  組卷：121引用：7難度：0.5

  解析

[選修4—5：不等式選講]

• 23．已知函數(shù)f（x）=|x-a|+|x-b|+|x-c|．
  （1）若a=b=c,且{x|f（x）＜6}={x|m＜x＜6}，求m的值；
  （2）若b-1≤a≤b+2，d-3≤c≤d+2，證明：f（x）≤5+|x-d|+|2x-2b|．
  組卷：24引用：3難度：0.5

  解析