2023年廣東省廣州市花都區秀全中學高考數學適應性試卷（四）

一、選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的，請把答案填涂在答題卡相應位置上.

• 1．若集合A={x|x=4k-3，k∈N}，B={x|（x+3）（x-9）≤0}，則A∩B的元素個數為（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：332引用：7難度：0.9

  解析

• 2．已知2-i（i是虛數單位）是關于x的方程x²+bx+c=0（b,c∈R）的一個根，則b+c=（　　）

  A．9

  B．1

  C．-7

  D．2i-5
  組卷：117引用：6難度：0.8

  解析

• 3．設命題p：?x₀＞0，sinx₀＞1+cosx₀，則￢p為（　　）

  A．?x≤0，sinx＞1+cosx	B．?x＞0，sinx＜1+cosx
  C．?x＞0，sinx≤1+cosx	D．?x≤0，sinx≤1+cosx
  組卷：166引用：7難度：0.7

  解析

• 4．中國古代許多著名數學家對推導高階等差數列的求和公式很感興趣，創造并發展了名為“垛積術”的算法，展現了聰明才智．南宋數學家楊輝在《詳解九章算法》和《算法通變本末》中，所討論的二階等差數列與一般等差數列不同，前后兩項之差并不相等，但是后項減前項之差組成的新數列是等差數列．現有一個“堆垛”，共50層，第一層2個小球，第二層5個小球，第三層10個小球，第四層17個小球，…，按此規律，則第50層小球的個數為（　　）

  A．2400

  B．2401

  C．2500

  D．2501
  組卷：214引用：9難度：0.6

  解析

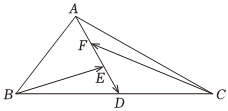• 5．如圖，在△ABC中，點D為線段BC的中點，點E，F分別是線段AD上靠近D，A的三等分點，則

  AD

  =（　　）

  A． - BE - 1 3 CF

  B． - 1 3 BE - CF

  C． - BE - CF

  D． - 4 9 BE - CF
  組卷：383引用：5難度：0.7

  解析

• 6．《易經》是中國傳統文化中的精髓．如圖是易經先天八卦圖（記憶口訣：乾三連、坤六斷、巽下斷、震仰孟、坎中滿、離中虛、畏覆碗、兌上缺），每一卦由三根線組成（“______”表示一根陽線，“——”表示一根陰線），現從八卦中任取兩卦，已知兩卦中至少有一卦恰有兩根陽線，求兩卦的6根線中恰有3根陽線的概率為（　　）

  A． 3 28

  B． 1 3

  C． 1 2

  D． 3 5
  組卷：62引用：1難度：0.8

  解析

• 7．已知函數f（x）=sin（ωx）+2

  3

  cos²（

  ωx

  2

  ）-

  3

  （ω＞0）為奇函數，且f（x）圖象的相鄰兩對稱軸間的距離為

  π

  2

  ．若將函數f（x）的圖象向右平移

  π

  3

  個單位后得到g（x）的圖象，且當x∈[0，

  π

  4

  ]時，不等式2m²-m≥g（x）恒成立，則m的取值范圍為（　　）

  A．（-∞，-1]∪[ 1 2 ，+∞）	B．（-∞，- 1 2 ]∪[1，+∞）
  C．（-∞， 1 - 17 4 ]∪[ 1 + 17 4 ，+∞）	D．（-∞，0]∪[ 1 2 ，+∞）
  組卷：79引用：4難度：0.6

  解析

四、解答題：本大題共6小題，共70分.請在答題卡指定區域內作答，解答時應寫出必要的文字說明，證明過程或演算步驟.

• 21．已知雙曲線W：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  ′

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁、F₂，點N（0，b），右頂點是M，且

  MN

  ?

  M

  F

  2

  =

  -

  1

  ，∠NMF₂=120°．
  （Ⅰ）求雙曲線的方程；
  （Ⅱ）過點Q（0，-2）的直線l交雙曲線W的右支于A、B兩個不同的點（B在A、Q之間），若點H（7，0）在以線段AB為直徑的圓的外部，試求△AQH與△BQH面積之比λ的取值范圍．
  組卷：392引用：9難度：0.1

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  e

  x

  -

  1

  6

  a

  x

  3

  （a為非零常數），記f_n+1（x）=f'_n（x）（n∈N），f₀（x）=f（x）．
  （1）當x＞0時，f（x）≥0恒成立，求實數a的最大值；
  （2）當a=1時，設

  g

  n

  （

  x

  ）

  =

  n

  ∑

  i

  =

  2

  f

  i

  （

  x

  ）

  ，對任意的n≥3，當x=t_n時，y=g_n（x）取得最小值，證明：g_n（t_n）＞0且所有點（t_n，g_n（t_n））在一條定直線上．
  組卷：76引用：5難度：0.3

  解析