人教A新版必修1《3.2.2 奇偶性》2019年同步練習卷（三）

練習

• 1．若f（x）=ax²+bx+c（a≠0）是偶函數，則g（x）=ax³+bx²+cx是

  ．
  組卷：41引用：2難度：0.7

  解析

• 2．已知函數f（x）=

  1 ， x ＞ 0

  - 1 ， x ＜ 0

  ，則函數f（x）是

  函數．（填“奇”或“偶”）．
  組卷：32引用：1難度：0.8

  解析

• 3．若函數f（x）=2x²+（a-1）x+2是偶函數，則實數a的值是

  ．
  組卷：81引用：1難度：0.8

  解析

• 4．如圖，給出偶函數f（x）的局部圖象，則使f（x）＞0的x的集合是

  ．
  
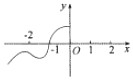  組卷：59引用：1難度：0.8

  解析

• 5．函數f（x）是定義域為R的奇函數，當x＞0時f（x）=-x+1，則當x＜0時，f（x）的表達式為（　　）

  A．f（x）=-x+1

  B．f（x）=-x-1

  C．f（x）=x+1

  D．f（x）=x-1
  組卷：1247引用：32難度：0.9

  解析

• 6．已知偶函數f（x）在區間[0，+∞）單調遞增，則滿足f（2x-1）＜f（

  1

  3

  ）的x取值范圍是（　　）

  A．（ 1 3 ， 2 3 ）

  B．[ 1 3 ， 2 3 ）

  C．（ 1 2 ， 2 3 ）

  D．[ 1 2 ， 2 3 ）
  組卷：2859引用：106難度：0.7

  解析

• 7．若函數y=f（x）為偶函數，且在（0，+∞）上是減函數，有f（5）=0，

  則

  f

  （

  x

  ）

  +

  f

  （

  -

  x

  ）

  2

  x

  ＜

  0

  的解集為

  ．
  組卷：70引用：3難度：0.5

  解析

練習

• 22．已知f（x）為偶函數，且f（x）在[0，+∞）單調遞增，若f（ax+1）-f（x-2）≤0在

  x

  ∈

  [

  1

  2

  ，

  1

  ]

  上恒成立，則實數a的取值范圍是

   

  ．
  組卷：120引用：4難度：0.5

  解析

• 23．已知y=f（x）是定義在（-∞，+∞）上的奇函數，且在[0，+∞）上單調遞增．
  （1）求證：函數在（-∞，0）上單調遞增．
  （2）如果f（

  1

  2

  ）=1，解不等式-1＜f（2x+1）≤0．
  組卷：45引用：1難度：0.6

  解析