當前位置：試卷中心 > 試卷詳情

2023年貴州省銅仁市思南中學高考數學模擬試卷

發布：2024/7/14 8:0:9

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知定義在[0，+∞）上的函數f（x）滿足
f
（
x
）
=
1
2
f
（
x
+
2
）
，且當x∈[0，2）時，f（x）=-x²+2x.設f（x）在[2n-2，2n]上的最大值為
a
n
（
n
∈
N
*
）
，且數列{a_n}的前n項和為S_n．若對于任意正整數n不等式k（S_n+1）≥2n-9恒成立，則實數k的取值范圍為（　　）
A．[0，+∞） B．
[
1
32
，
+
∞
）
C．
[
3
64
，
+
∞
）
D．
[
7
64
，
+
∞
）
組卷：357引用：2難度：0.4
解析
2．已知{a_n}為正項等比數列，S_n是它的前n項和．若a₁=16，且a₄與a₇的等差中項為
9
8
，則S₅的值（　　）
A．29 B．31 C．33 D．35
組卷：136引用：6難度：0.7
解析
3．已知x=0是函數f（x）=x（ax-tanx）的極大值點，則a的取值范圍是（　　）
A．（-∞，-1） B．（-∞，1] C．[0，+∞） D．[1，+∞）
組卷：200引用：3難度：0.5
解析
4．已知函數f（x）=x²-3x+5，g（x）=ax-lnx,若對?x∈（0，e），?x₁，x₂∈（0，e）且x₁≠x₂，使得f（x）=g（x_i）（i=1，2），則實數a的取值范圍是（　　）
A．
（
1
e
，
6
e
）
B．
[
1
e
，
e
7
4
）
C．
[
6
e
，
e
7
4
）
D．
（
0
，
1
e
]
∪
[
6
e
，
e
7
4
）
組卷：823引用：14難度：0.4
解析
5．已知集合A={y|y=
x
2
-
1
}，B={x|y=lg（x-2x²）}，則?_R（A∩B）=（　　）
A．[0，
1
2
） B．（-∞，0）∪[
1
2
，+∞）
C．（0，
1
2
） D．（-∞，0]∪[
1
2
，+∞）
組卷：152引用：6難度：0.9
解析
6．已知函數
f
（
x
）
=
x
3
+
sinx
（
1
+
x
）
（
m
-
x
）
+
e
x
+
e
-
x
為奇函數，則m=（　　）
A．
1
2
B．1 C．2 D．3
組卷：159引用：2難度：0.8
解析
7．已知集合A={x|x+1≤0}，B={x|x≥a}，若A∪B=R，則實數a的值可以為（　　）
A．2 B．1 C．0 D．-2
組卷：467引用：7難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知橢圓C的焦點在x軸上，且順次連接四個頂點恰好構成了一個邊長
3
為且面積為2
2
的菱形．
（1）求橢圓C的方程；
（2）設M（-3，0），過橢圓C右焦點F的直線l交于A、B兩點，若對滿足條件的任意直線l,不等式
MA
?
MB
≤λ（λ∈R）恒成立，求λ的最小值．
組卷：44引用：3難度：0.4
解析
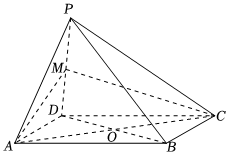22．如圖，四棱錐P-ABCD中，底面ABCD是菱形，對角線AC，BD交于點O，M為棱PD的中點，MA=MC．求證：
（1）PB∥平面AMC；
（2）平面PBD⊥平面AMC．
組卷：806引用：2難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ 1 e ， 6 e ）	B． [ 1 e ， e 7 4 ）
C． [ 6 e ， e 7 4 ）	D．（ 0 ， 1 e ] ∪ [ 6 e ， e 7 4 ）

A．[0， 1 2 ）	B．（-∞，0）∪[ 1 2 ，+∞）
C．（0， 1 2 ）	D．（-∞，0]∪[ 1 2 ，+∞）

2023年貴州省銅仁市思南中學高考數學模擬試卷

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

2．已知{an}為正項等比數列，Sn是它的前n項和．若a1=16，且a4與a7的等差中項為98，則S5的值（ ）

3．已知x=0是函數f（x）=x（ax-tanx）的極大值點，則a的取值范圍是（ ）

4．已知函數f（x）=x2-3x+5，g（x）=ax-lnx,若對?x∈（0，e），?x1，x2∈（0，e）且x1≠x2，使得f（x）=g（xi）（i=1，2），則實數a的取值范圍是（ ）

5．已知集合A={y|y=x2-1}，B={x|y=lg（x-2x2）}，則?R（A∩B）=（ ）

6．已知函數f（x）=x3+sinx（1+x）（m-x）+ex+e-x為奇函數，則m=（ ）

7．已知集合A={x|x+1≤0}，B={x|x≥a}，若A∪B=R，則實數a的值可以為（ ）

三、解答題：共70分.解答應寫出文字說明、證明過程或演算步驟.

22．如圖，四棱錐P-ABCD中，底面ABCD是菱形，對角線AC，BD交于點O，M為棱PD的中點，MA=MC．求證：（1）PB∥平面AMC；（2）平面PBD⊥平面AMC．

2．已知{a_n}為正項等比數列，S_n是它的前n項和．若a₁=16，且a₄與a₇的等差中項為
9
8
，則S₅的值（　　）

3．已知x=0是函數f（x）=x（ax-tanx）的極大值點，則a的取值范圍是（　　）

4．已知函數f（x）=x²-3x+5，g（x）=ax-lnx,若對?x∈（0，e），?x₁，x₂∈（0，e）且x₁≠x₂，使得f（x）=g（x_i）（i=1，2），則實數a的取值范圍是（　　）

5．已知集合A={y|y=
x
2
-
1
}，B={x|y=lg（x-2x²）}，則?_R（A∩B）=（　　）

6．已知函數
f
（
x
）
=
x
3
+
sinx
（
1
+
x
）
（
m
-
x
）
+
e
x
+
e
-
x
為奇函數，則m=（　　）

7．已知集合A={x|x+1≤0}，B={x|x≥a}，若A∪B=R，則實數a的值可以為（　　）

22．如圖，四棱錐P-ABCD中，底面ABCD是菱形，對角線AC，BD交于點O，M為棱PD的中點，MA=MC．求證：
（1）PB∥平面AMC；
（2）平面PBD⊥平面AMC．