2023年陜西省西安市國際港務(wù)區(qū)鐵一中陸港中學(xué)中考數(shù)學(xué)七模試卷

一、選擇題（每題3分，共24分）

• 1．實(shí)數(shù)

  81

  16

  的算術(shù)平方根是（　　）

  A． 81 16

  B． 3 2

  C． ± 81 16

  D． ± 3 2
  組卷：686引用：1難度：0.6

  解析

• 2．既是軸對(duì)稱圖形又是中心對(duì)稱圖形的是（　　）

  A．菱形

  B．等邊三角形

  C．平行四邊形

  D．扇形
  組卷：71引用：2難度：0.9

  解析

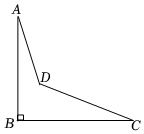• 3．如圖是一個(gè)零件示意圖，經(jīng)測量得知∠A=17°，∠B=90°，∠D=130°25'，則∠C的度數(shù)為（　　）

  A．23°25'

  B．33°

  C．27°

  D．23°
  組卷：263引用：1難度：0.7

  解析

• 4．化簡：

  x

  x

  -

  y

  -

  y

  x

  +

  y

  ，結(jié)果正確的是（　　）

  A．1

  B． x 2 + y 2 x 2 - y 2

  C． x - y x + y

  D．x2+y2
  組卷：1671引用：9難度：0.9

  解析

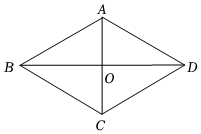• 5．如圖，四邊形ABCD中，AC⊥BD于點(diǎn)O，則下列條件能判定該四邊形是菱形的是（　　）

  A．AB=BC	B．AC=BD
  C．AB∥CD	D．AC、BD互相平分
  組卷：293引用：2難度：0.5

  解析

• 6．已知直線l₁：y=kx+b（k≠0）與直線l_2：y=k₁x-6（k₁＜0）在第三象限交于點(diǎn)M，若直線l₁與x軸的交點(diǎn)為B（3，0），則k的取值范圍是（　　）

  A．-2＜k＜2

  B．-2＜k＜0

  C．0＜k＜4

  D．0＜k＜2
  組卷：3487引用：16難度：0.2

  解析

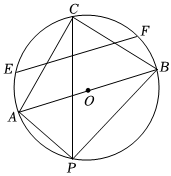• 7．如圖，AB是半徑為4的⊙O的直徑，P是圓上異于A，B的任意一點(diǎn)，∠APB的平分線交⊙O于點(diǎn)C，連接AC和BC，△ABC的中位線所在的直線與⊙O相交于點(diǎn)E、F，則EF的長是（　　）

  A． 4 3

  B． 2 3

  C．3

  D． 2 5
  組卷：427引用：3難度：0.7

  解析

• 8．若一個(gè)二次函數(shù)y=ax²+bx+c（a＞0）的圖象經(jīng)過五個(gè)點(diǎn)A（-1，n）、B（3，n）、C（0，y₁）、D（-2，y₂）和E（2.5，y₃），則下列關(guān)系正確的是（　　）

  A．y1＞y2＞y3

  B．y2＞y3＞y1

  C．y1＜y2＜y3

  D．y3＞y1＞y2
  組卷：672引用：5難度：0.6

  解析

三、解答題

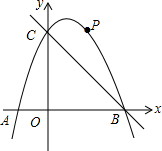• 25．如圖，在平面直角坐標(biāo)系中，二次函數(shù)y=-x²+bx+c的圖象與x軸交于A、B兩點(diǎn)，與y軸交于C（0，3），A點(diǎn)在原點(diǎn)的左側(cè)，B點(diǎn)的坐標(biāo)為（3，0）．點(diǎn)P是拋物線上一個(gè)動(dòng)點(diǎn)，且在直線BC的上方．
  （1）求這個(gè)二次函數(shù)的表達(dá)式．
  （2）連接PO、PC，并把△POC沿CO翻折，得到四邊形POP′C，那么是否存在點(diǎn)P，使四邊形POP′C為菱形？若存在，請(qǐng)求出此時(shí)點(diǎn)P的坐標(biāo)；若不存在，請(qǐng)說明理由．
  （3）當(dāng)點(diǎn)P運(yùn)動(dòng)到什么位置時(shí)，四邊形ABPC的面積最大，并求出此時(shí)點(diǎn)P的坐標(biāo)和四邊形ABPC的最大面積．
  組卷：1115引用：8難度：0.3

  解析

• 26．問題提出：
  （1）如圖①，若∠A=120°，AB=6，AC=5，則△ABC的面積為

  ；
  問題發(fā)現(xiàn)：
  （2）如圖②，在四邊形ABCD中，∠DAB=30°，∠BCD=60°，AD=AB，CD=CB=60，點(diǎn)M，N分別為邊CB，CD上兩動(dòng)點(diǎn)，且CM+CN=40，連接AM，AN，試說明四邊形AMCN的面積是定值；
  問題解決：
  （3）如圖③是一塊平行四邊形空地，其中AB=1000m,AD=600m,∠DAB=60°，點(diǎn)M，N分別為邊CB，CD上兩點(diǎn)，且CM+CN=800m,連接AM，MN，AN．公司規(guī)劃在△AND區(qū)域修建一座購物商城，在△CMN區(qū)域修建一個(gè)顧客休息中心，在△ABM區(qū)修建小吃城，最后中間△AMN區(qū)域進(jìn)行綠化．公司為了利益最大化，綠化面積即△AMN的面積盡可能小．請(qǐng)你計(jì)算出綠化面積的最小值和CM的長度．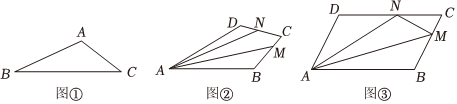
  
  組卷：107引用：1難度：0.2

  解析