2022-2023學年北京二中高一（下）期中數學試卷

一、選擇題共10小題，每小題4分，共40分，在每小題列出的四個選項中，選出符合題目要求的一項.

• 1．復數z=2+i,則z在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：29引用：6難度：0.9

  解析

• 2．在平行四邊形ABCD中，

  AB

  -

  AD

  等于（　　）

  A． AC

  B． DB

  C． CA

  D． BD
  組卷：159引用：2難度：0.8

  解析

• 3．已知角α滿足sinα＜0，tanα＜0，則角α的終邊所在的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：284引用：4難度：0.8

  解析

• 4．為了得到函數

  y

  =

  sin

  （

  x

  +

  π

  4

  ）

  的圖象，只需把

  y

  =

  sin

  （

  x

  -

  π

  4

  ）

  的圖象上所有的點（　　）

  A．向左平移 π 2 個單位長度	B．向右平移 π 4 個單位長度
  C．向左平移 π 4 個單位長度	D．向右平移 π 2 個單位長度
  組卷：391引用：6難度：0.9

  解析

• 5．在△ABC中，若a=

  3

  ，sinA=

  3

  2

  ，B=

  π

  6

  ，則b=（　　）

  A．1

  B．2 3

  C．2

  D． 3
  組卷：215引用：3難度：0.8

  解析

• 6．已知向量

  a

  =（m,2），

  b

  =（3，1），若（

  a

  +3

  b

  ）∥

  b

  ，則實數m=（　　）

  A．3

  B．6

  C．-3

  D．-6
  組卷：249引用：2難度：0.8

  解析

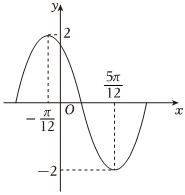• 7．函數y=Asin（ωx+φ）（A＞0，0＜φ＜π）在一個周期內的圖象如圖所示，則此函數的解析式為（　　）

  A． y = 2 sin （ 2 x + 2 π 3 ）	B． y = 2 sin （ 2 x + π 3 ）
  C． y = sin （ x + 7 π 12 ）	D． y = sin （ x + 11 π 12 ）
  組卷：281引用：7難度：0.5

  解析

三、解答題共6道題，共85分，解答應寫出文字說明，證明過程或演算步驟.

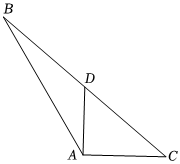• 20．在△ABC中，cosA=

  -

  1

  2

  ，a=2

  7

  ，b=2．
  （1）求c；
  （2）設D為BC邊上一點，且AD⊥AC，求△ABD的面積．
  組卷：184引用：4難度：0.6

  解析

• 21．對于函數y=f（x），x∈D₁，y=g（x），x∈D₂及實數m,若存在x₁∈D₁，x₂∈D₂，使得f（x₁）+g（x₂）=m,則稱函數f（x）與g（x）具有“m關聯”性質．
  （1）分別判斷下列兩組函數是否具有“2關聯”性質，直接寫出結論：
  ①f（x）=x,x∈[-1，1]；g（x）=-x,x∈[-1，1]；
  ②f（x）=e^x，x≥1；g（x）=e^x，x≤l；
  （2）若f（x）=sinx與g（x）=cos2x具有“m關聯”性質，求m的取值范圍；
  （3）已知a＞0，f（x）為定義在R上的奇函數，且滿足：
  ①在[0，2a]上，當且僅當x=

  a

  2

  時，f（x）取得最大值1；
  ②對任意x∈R，有f（a+x）+f（a-x）=0．
  求證：y₁=sinπx+f（x）與y₂=cosπx-f（x）不具有“4關聯”性質．
  組卷：78引用：4難度：0.6

  解析