當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省鹽城市東臺市第五教育聯盟七年級（下）第二次月考數學試卷（5月份）

發布：2024/7/25 8:0:9

一、選擇題（本大題共8小題，每小題3分，共24分）

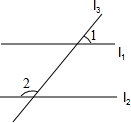1．如圖，已知l₁∥l₂，∠1=50°，則∠2的度數是（　　）
A．50° B．100° C．120° D．130°
組卷：119引用：8難度：0.9
解析
2．下列運算正確的是（　　）
A．a³?a⁴=a¹² B．（a³）²=a⁵
C．（a²b³）²=a⁴b⁵ D．a⁷÷a³=a⁴
組卷：75引用：3難度：0.7
解析
3．下列從左到右的變形中，是因式分解的是（　　）
A．（x+3）²=x²+6x+9 B．a²-4=（a+2）（a-2）
C．3xy²=3x?y?y D．x²+2x+2=x（x+2）+2
組卷：288引用：2難度：0.5
解析
4．下列方程是二元一次方程的是（　　）
A．2x-4=x B．x-2y=6 C．
x
+
3
y
=
1
D．xy=5
組卷：132引用：4難度：0.9
解析
5．本屆運動會共有24個隊、260名運動員參加其中的籃球、排球比賽，其中籃球隊每隊10名，排球隊每隊12名．若設參賽的籃球隊有x支，參賽的排球隊有y支，根據題意，可列方程組（　　）
A．
x
+
y
=
24
10
x
+
12
y
=
260
B．
y
=
24
+
x
10
x
+
12
y
=
260
C．
x
+
y
=
260
10
x
+
12
y
=
24
D．
x
=
24
-
y
12
x
+
10
y
=
260
組卷：446引用：5難度：0.7
解析
6．已知a＞b,則下列不等式一定成立的是（　　）
A．a+2＞b+3 B．a-2＞b-2 C．-2a＞-2b D．
a
2
＜
b
2
組卷：193引用：8難度：0.7
解析
7．若方程組
a
1
x
+
b
1
y
=
c
1
a
2
x
+
b
2
y
=
c
2
的解是
x
=
4
y
=
-
2
，則方程組
3
a
1
x
+
2
b
1
y
=
a
1
+
c
1
3
a
2
x
+
2
b
2
y
=
a
2
+
c
2
?的解是（　　）
A．
x
=
-
1
y
=
1
B．
x
=
-
1
y
=
-
1
C．
x
=
5
3
y
=
-
1
D．
x
=
5
3
y
=
1
組卷：223引用：1難度：0.8
解析
8．已知關于x的不等式組
x
＞
a
x
＜
4
?恰有3個整數解，則a的取值范圍是（　　）
A．1＜a＜2 B．0＜a＜1 C．0≤a＜1 D．0＜a≤1
組卷：134引用：1難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共10小題，共72分）

25．第24屆冬季奧運會于2022年02月04日至2022年02月20日在中華人民共和國北京市和張家口市聯合舉行，這是中國歷史上第一次舉辦冬季奧運會．冬奧會吉祥物“冰墩墩”和“雪容融”陶制品分為小套裝和大套裝兩種．已知購買2個小套裝比購買1個大套裝少用20元；購買3個小套裝和2個大套裝，共需390元．
（1）求這兩種套裝的單價分別為多少元？
（2）某校計劃用1500元的資金購買這種陶制品小套裝和大套裝共20個作為獎品，則該校最多可以購買大套裝多少個？
組卷：438引用：5難度：0.5
解析
26．【閱讀材料】配方法是數學中重要的一種思想方法．它是指將一個式子的某一部分通過恒等變形化為完全平方式或幾個完全平方式的和的方法．這種方法常被用到代數式的變形中，并結合非負數的意義來解決一些問題．
我們定義：一個整數能表示成a²+b²（a,b是整數）的形式，則稱這個數為“完美數”．例如，5是“完美數”．理由：因為5=2²+1²，所以5是“完美數”．
【解決問題】
（1）數53
“完美數”（填“是”或“不是”）；
【探究問題】
（2）已知x²+y²-4x+2y+5=0，則x+y=
；
（3）已知S=2x²+y²+2xy+12x+k（x,y 是整數，k是常數），要使S為“完美數”，試求出符合條件的k值，并說明理由；
【拓展結論】
（4）已知實數x、y滿足
-
x
2
+
7
2
x
+
y
-
3
=
0
，求x-2y的最大值．
組卷：1544引用：5難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．a³?a⁴=a¹²	B．（a³）²=a⁵
C．（a²b³）²=a⁴b⁵	D．a⁷÷a³=a⁴

A．（x+3）²=x²+6x+9	B．a²-4=（a+2）（a-2）
C．3xy²=3x?y?y	D．x²+2x+2=x（x+2）+2

2022-2023學年江蘇省鹽城市東臺市第五教育聯盟七年級（下）第二次月考數學試卷（5月份）

一、選擇題（本大題共8小題，每小題3分，共24分）

1．如圖，已知l1∥l2，∠1=50°，則∠2的度數是（ ）

2．下列運算正確的是（ ）

3．下列從左到右的變形中，是因式分解的是（ ）

4．下列方程是二元一次方程的是（ ）

5．本屆運動會共有24個隊、260名運動員參加其中的籃球、排球比賽，其中籃球隊每隊10名，排球隊每隊12名．若設參賽的籃球隊有x支，參賽的排球隊有y支，根據題意，可列方程組（ ）

6．已知a＞b,則下列不等式一定成立的是（ ）

7．若方程組a1x+b1y=c1a2x+b2y=c2的解是x=4y=-2，則方程組3a1x+2b1y=a1+c13a2x+2b2y=a2+c2?的解是（ ）

8．已知關于x的不等式組x＞ax＜4?恰有3個整數解，則a的取值范圍是（ ）

三、解答題（本大題共10小題，共72分）

1．如圖，已知l₁∥l₂，∠1=50°，則∠2的度數是（　　）

2．下列運算正確的是（　　）

3．下列從左到右的變形中，是因式分解的是（　　）

4．下列方程是二元一次方程的是（　　）

5．本屆運動會共有24個隊、260名運動員參加其中的籃球、排球比賽，其中籃球隊每隊10名，排球隊每隊12名．若設參賽的籃球隊有x支，參賽的排球隊有y支，根據題意，可列方程組（　　）

6．已知a＞b,則下列不等式一定成立的是（　　）

7．若方程組
a
1
x
+
b
1
y
=
c
1
a
2
x
+
b
2
y
=
c
2
的解是
x
=
4
y
=
-
2
，則方程組
3
a
1
x
+
2
b
1
y
=
a
1
+
c
1
3
a
2
x
+
2
b
2
y
=
a
2
+
c
2
?的解是（　　）

8．已知關于x的不等式組
x
＞
a
x
＜
4
?恰有3個整數解，則a的取值范圍是（　　）