2023年重慶市萬州第二高級中學高考數學二診試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設全集U={1，2，3，4，5}，A={1，2}，?_UA=（　　）

  A．{1，2，3}

  B．{2，3，4}

  C．{3，4，5}

  D．{4，5}
  組卷：106引用：2難度：0.9

  解析

• 2．設a,b為兩條直線，α，β為兩個平面，則下列說法正確的是（　　）

  A．若a∥α，b?α，則a∥b	B．若a∥b,a∥α，則b∥α
  C．若a⊥α，a∥β，則α⊥β	D．若a⊥α，a⊥b,則b∥α
  組卷：65引用：6難度：0.6

  解析

• 3．△ABC的內角A，B，C的對邊分別為a,b,c,a=3，b=4，

  c

  =

  13

  ，點D，E分別是邊BC，BA的中點，且AD，CE交于點O，則四邊形BDOE的面積為（　　）

  A． 2 3 3

  B． 4 3 5

  C． 3

  D． 5 3 4
  組卷：121引用：4難度：0.5

  解析

• 4．（x²-

  2

  x

  3

  ）⁵展開式中的常數項為（　　）

  A．80

  B．-80

  C．40

  D．-40
  組卷：1618引用：30難度：0.7

  解析

• 5．已知定義在R上的奇函數f（x）滿足：當x≥0時，f（x）=x³，若不等式f（-4t）＞f（2m+mt²）對任意實數t恒成立，則實數m的取值范圍是（　　）

  A．（-∞，- 2 ）	B．（- 2 ，0）
  C．（-∞，0）∪（ 2 ，+∞）	D．（-∞，- 2 ）∪（ 2 ，+∞）
  組卷：373引用：6難度：0.5

  解析

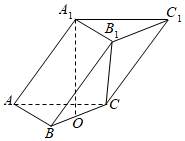• 6．在如圖所示的三棱柱ABC-A₁B₁C₁中，已知AA₁=8，AC=AB=5，BC=6，點A₁在底面ABC上的射影是線段BC的中點O，則直線B₁C與直線A₁O所成角的正切值為（　　）

  A． 7

  B． 39 6

  C． 2 39 13

  D． 7 7
  組卷：165引用：2難度：0.7

  解析

• 7．設

  a

  =

  1

  101

  ，b=ln1.01，c=e^0.01-1，則（　　）

  A．a＜b＜c

  B．b＜c＜a

  C．b＜a＜c

  D．c＜a＜b
  組卷：845引用：2難度：0.4

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．設橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的右焦點為F₁，離心率為

  2

  2

  ，過點F₁且與x軸垂直的直線被橢圓截得的線段長為

  2

  ．
  （1）求橢圓C的方程；
  （2）若y²=4x上存在兩點M，N，橢圓C上存在兩個點P，Q，滿足：P，Q，F₁三點共線，M，N，F₁三點共線且PQ⊥MN，求四邊形PMQN的面積的最小值．
  組卷：128引用：3難度：0.5

  解析

• 22．已知函數

  g

  （

  x

  ）

  =

  t

  （

  lnx

  -

  x

  ）

  -

  lnx

  +

  x

  2

  2

  +

  t

  （

  t

  ＞

  2

  ）

  ．
  （1）求函數g（x）的極值；
  （2）若g（m）-g（1）=0且m≠1，證明：?x∈（1，m]，tlnx-lnx-x+1＞0．
  組卷：77引用：2難度：0.3

  解析