2021-2022學年廣東省廣州市八區高二（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．直線y=

  3

  x+2的傾斜角是（　　）

  A． 2 π 3

  B． π 3

  C． 5 π 6

  D． π 6
  組卷：562引用：8難度：0.9

  解析

• 2．已知圓C的方程為x²+y²+2x-4y-4=0，則圓心C的坐標為（　　）

  A．（-1，2）

  B．（1，-2）

  C．（-2，4）

  D．（2，-4）
  組卷：809引用：4難度：0.8

  解析

• 3．在等差數列{a_n}中，已知a₃+a₄=12，則數列{a_n}的前6項之和為（　　）

  A．12

  B．32

  C．36

  D．72
  組卷：380引用：7難度：0.8

  解析

• 4．已知點P（-1，2）到直線l：4x-3y+m=0的距離為1，則m的值為（　　）

  A．-5或-15

  B．-5或15

  C．5或-15

  D．5或15
  組卷：812引用：4難度：0.8

  解析

• 5．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的漸近線方程為y=±

  3

  3

  x,則該雙曲線的離心率等于（　　）

  A． 2 3 3

  B． 4 3

  C．2

  D．4
  組卷：936引用：4難度：0.8

  解析

• 6．已知△ABC的周長為14，頂點B，C的坐標分別為（0，3），（0，-3），則點A的軌跡方程為（　　）

  A． x 2 16 + y 2 7 =1（x≠0）	B． y 2 16 + x 2 7 =1（y≠0）
  C． x 2 16 + y 2 7 =1（y≠0）	D． y 2 16 + x 2 7 =1（x≠0）
  組卷：225引用：3難度：0.7

  解析

• 7．在四面體OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，且

  OP

  =2

  PA

  ，

  BQ

  =

  QC

  ，則

  PQ

  等于（　　）

  A．- 2 3 a - 1 2 b + 1 2 c	B．- 2 3 a + 1 2 b + 1 2 c
  C． 2 3 a + 1 2 b - 1 2 c	D． 2 3 a - 1 2 b + 1 2 c
  組卷：231引用：3難度：0.8

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

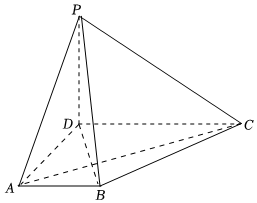• 21．如圖，在四棱錐P-ABCD中，底面ABCD為直角梯形，平面PCD⊥平面ABCD，AD⊥CD，PD⊥AC．
  （1）證明：PD⊥平面ABCD；
  （2）已知AB=1，CD=2，AD=

  2

  ，且直線PB與平面PCD所成角的正弦值為

  3

  3

  ，求平面BDP與平面BCP夾角的余弦值．
  組卷：278引用：3難度：0.5

  解析

• 22．動點M（x,y）與定點F（

  3

  ，0）的距離和它到定直線l：x=

  3

  3

  的距離的比是

  3

  ，記動點M的軌跡為曲線C．
  （1）求曲線C的方程；
  （2）已知過點P（-1，1）的直線與曲線C相交于兩點A，B，請問點P能否為線段AB的中點，并說明理由．
  組卷：383引用：3難度：0.5

  解析