2021-2022學年福建師大二附中高一（下）月考數學試卷（3月份）

一、選擇題：本大題共8小題，每小題5分，共40分

• 1．已知全集U={1，2，3，4，5}，集合M={1，3，5}，?_UN={3，4}，則M∩N=（　　）

  A．{1}

  B．{1，2}

  C．{1，5}

  D．{1，2，5}
  組卷：57引用：3難度：0.9

  解析

• 2．已知向量

  AB

  =

  （

  7

  ，

  6

  ）

  ，

  BC

  =

  （

  -

  3

  ，

  m

  ）

  ，

  AD

  =

  （

  -

  1

  ，

  2

  m

  ）

  ，若A，C，D三點共線，則m=（　　）

  A． 3 2

  B． 2 3

  C． - 3 2

  D． - 2 3
  組卷：523引用：8難度：0.8

  解析

• 3．下列說法正確的個數是（　　）
  （1）溫度、速度、位移、功這些物理量是向量；
  （2）零向量沒有方向；
  （3）向量的模一定是正數；
  （4）非零向量的單位向量是唯一的．

  A．0

  B．1

  C．2

  D．3
  組卷：815引用：4難度：0.8

  解析

• 4．已知弧長為

  π

  3

  的弧所對的圓心角為

  π

  6

  ，則該弧所在的扇形面積為（　　）

  A． 3 π

  B． 1 3 π

  C． 2 3 π

  D． 4 3 π
  組卷：232引用：6難度：0.7

  解析

• 5．在△ABC中，內角A，B，C的對邊分別為a,b,c,已知c=5，B=

  2

  π

  3

  ，△ABC的面積為

  15

  3

  4

  ，則b=（　　）

  A．7 3

  B．7

  C．6 3

  D．6
  組卷：44引用：6難度：0.7

  解析

• 6．已知函數f（x）是定義在R上的奇函數，f（x）=f（x+4），且f（-1）=-1，則f（2020）+f（2021）=（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：329引用：4難度：0.8

  解析

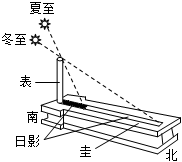• 7．如圖，圭表是中國古代通過測量日影長度來確定節令的儀器，也是作為指導漢族勞動人民農事活動的重要依據，它由“圭”和“表”兩個部件組成，圭是南北方向水平放置測定表影長度的刻板，表是與圭垂直的桿，正午時太陽照在表上，通過測量此時表在圭上的影長來確定節令．已知冬至和夏至正午時，太陽光線與圭所在平面所成角分別為α，β，測得表影長之差為l,那么表高為（　　）

  A． ltanαtanβ tanα - tanβ	B． l （ tanβ - tanα ） tanβtanα
  C． ltanβtanα tanβ - tanα	D． l （ tanα - tanβ ） tanαtanβ
  組卷：56引用：3難度：0.6

  解析

四、解答題：本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟

• 21．在△中，角A，B，C的對邊分別是a,b,c,且

  b

  +

  c

  =

  a

  （

  3

  sin

  C

  +

  cos

  C

  ）

  ．
  （1）求角A；
  （2）求sinB+sinC的最大值．
  組卷：275引用：2難度：0.5

  解析

• 22．已知向量

  a

  =（sinx,cosx），

  b

  =（sin（x-

  π

  6

  ），sinx），函數f（x）=2

  a

  ?

  b

  ，g（x）=f（

  πx

  4

  ）．
  （1）求f（x）在[

  π

  2

  ，π]上的最值，并求出相應的x的值；
  （2）計算g（1）+g（2）+g（3）+…+g（2014）的值；
  （3）已知t∈R，討論g（x）在[t,t+2]上零點的個數．
  組卷：549引用：5難度：0.1

  解析