2022-2023學年河北省保定市六校聯盟高二（下）聯考數學試卷（4月份）

一、選擇題：本題共8小題，每小題3分，共040分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x²＜9}，B={x|-1＜x＜5，x∈N}，則A∩B=（　　）

  A．（-1，3）

  B．（0，5）

  C．{1，2}

  D．{0，1，2}
  組卷：94引用：6難度：0.8

  解析

• 2．函數

  f

  （

  x

  ）

  =

  lo

  g

  2

  1

  x

  的導函數為（　　）

  A． f ′ （ x ） = ln 2 x	B． f ′ （ x ） = 1 xln 2
  C． f ′ （ x ） = - ln 2 x	D． f ′ （ x ） = - 1 xln 2
  組卷：321引用：8難度：0.7

  解析

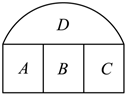• 3．如圖，提供4種不同的顏色給圖中A，B，C，D四塊區域涂色，若相鄰的區域不能涂同一種顏色，則不同的涂法共有（　　）種

  A．12

  B．36

  C．48

  D．72
  組卷：234引用：4難度：0.5

  解析

• 4．設函數

  f

  （

  x

  ）

  =

  1

  3

  x

  -

  lnx

  （

  x

  ＞

  0

  ）

  ，則y=f（x）（　　）

  A．在區間 （ 1 e ， 1 ） 遞減	B．在區間（0，3）上遞增
  C．在點x=3處有極大值	D．在區間（3，+∞）上遞減
  組卷：117引用：1難度：0.8

  解析

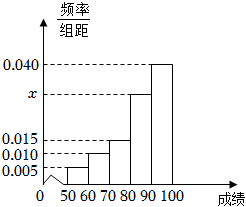• 5．某中學全體學生參加了數學競賽，隨機抽取了400名學生進行成績統計，發現抽取的學生的成績都在50分至100分之間，進行適當分組后（每組為左閉右開的區間），畫出頻率分布直方圖如圖所示，下列說法正確的是（　　）

  A．直方圖中x的值為0.035

  B．在被抽取的學生中，成績在區間[70，80）的學生數為30人

  C．估計全校學生的平均成績為83分

  D．估計全校學生成績的樣本數據的80%分位數約為95分
  組卷：375引用：7難度：0.8

  解析

• 6．某企業的一批產品由一等品零件、二等品零件混裝而成，每包產品均含有10個零件．小張到該企業采購，利用如下方法進行抽檢：從該企業產品隨機抽取1包產品，再從該包產品中隨機抽取4個零件，若抽取的零件都是一等品，則決定采購該企業產品；否則，拒絕采購．假設該企業這批產品中，每包產品含1個或2個二等品零件，其中含2個二等品零件的包數占10%，則小張決定采購該企業產品的概率為（　　）

  A． 1 30

  B． 43 75

  C． 3 50

  D． 1 10
  組卷：15引用：1難度：0.8

  解析

• 7．已知函數f（x）及其導函數f'（x）的定義域均為R，f（2x+3）是偶函數，記g（x）=f'（x），g（x+2）也是偶函數，則f'（2023）的值為（　　）

  A．-2

  B．0

  C．-1

  D．2
  組卷：64引用：1難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．法國數學家龐加萊是個喜歡吃面包的人，他每天都會到同一家面包店購買一個面包．該面包店的面包師聲稱自己所出售的面包的平均質量是1000 g,上下浮動不超過50 g.這句話用數學語言來表達就是：每個面包的質量服從期望為1000 g,標準差為50 g的正態分布．
  （1）已知如下結論：若X～N（μ，σ²），從X的取值中隨機抽取k（k∈N^*，k≥2）個數據，記這k個數據的平均值為Y，則隨機變量

  Y

  ～

  N

  （

  μ

  ，

  σ

  2

  k

  ）

  ．利用該結論解決下面問題．
  （ⅰ）假設面包師的說法是真實的，隨機購買25個面包，記隨機購買25個面包的平均值為Y，求P（Y≤980）；
  （ⅱ）龐加萊每天都會將買來的面包稱重并記錄，25天后，得到的數據都落在（950，1050）上，并經計算25個面包質量的平均值為978.72 g.龐加萊通過分析舉報了該面包師，從概率角度說明龐加萊舉報該面包師的理由；
  （2）假設有兩箱面包（面包除顏色外，其他都一樣），已知第一箱中共裝有6個面包，其中黑色面包有2個；第二箱中共裝有8個面包，其中黑色面包有3個．現隨機挑選一箱，然后從該箱中隨機取出2個面包．求取出黑色面包個數的分布列及數學期望．
  附：
  ①隨機變量η服從正態分布N（μ，σ²），則P（μ-σ≤η≤μ+σ）=0.6827，P（μ-2σ≤η≤μ+2σ）=0.9545，P（μ-3σ≤η≤μ+3σ）=0.9973；
  ②通常把發生概率小于0.05的事件稱為小概率事件，小概率事件基本不會發生．
  組卷：278引用：9難度：0.5

  解析

• 22．設函數f（x）=x²-ax-a²lnx.（a∈R）
  （1）當a=2時，討論函數y=f（x）的單調性；
  （2）曲線y=f（x）與直線y=m交于A（x₁，y₁），B（x₂，y₂）兩點，求證：

  f

  ′

  （

  x

  1

  +

  x

  2

  2

  ）

  ＞

  0

  ．
  組卷：18引用：1難度：0.5

  解析