2022年湖北省十一校高考數(shù)學(xué)第二次聯(lián)考試卷

一、單選題：本大題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

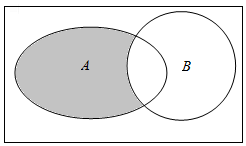• 1．若全集U=R，集合A={0，1，2，3，4，5}，B={x|x＜3}，則圖中陰影部分表示的集合為（　　）

  A．{0，1，2，3}

  B．{0，1，2}

  C．{3，4，5}

  D．{4，5}
  組卷：309引用：11難度：0.7

  解析

• 2．直線kx+y-2-3k=0與圓x²+y²-4x-5=0的位置關(guān)系是（　　）

  A．相離

  B．相切

  C．相交

  D．相交或相切
  組卷：313引用：4難度：0.8

  解析

• 3．祖暅原理：“冪勢(shì)既同，則積不容異”．它是中國(guó)古代一個(gè)涉及幾何體體積的問(wèn)題，意思是兩個(gè)同高的幾何體，如在等高處的截面面積恒相等，則體積相等．設(shè)A，B為兩個(gè)同高的幾何體，p：A，B的體積相等，q：A，B在等高處的截面面積恒相等，根據(jù)祖暅原理可知，p是q的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：258引用：12難度：0.9

  解析

• 4．定義：將24小時(shí)內(nèi)降水在平地上積水厚度（mm）來(lái)判斷降雨程度；其中小雨（0mm-10mm），中雨（10mm-25mm），大雨（25mm-50mm），暴雨（50mm-100mm）；小明用一個(gè)圓錐形容器接了24小時(shí)的雨水，則這天降雨屬于哪個(gè)等級(jí)（　　）

  A．小雨

  B．中雨

  C．大雨

  D．暴雨
  組卷：560引用：12難度：0.7

  解析

• 5．已知a,b為正實(shí)數(shù)，直線y=x-2a與曲線y=ln（x+b）相切，則

  1

  a

  +

  2

  b

  的最小值是（　　）

  A．8

  B． 4 2

  C．6

  D． 2 2
  組卷：477引用：9難度：0.5

  解析

• 6．如圖為宜昌市至喜長(zhǎng)江大橋，其纜索兩端固定在兩側(cè)索塔頂部，中間形成的平面曲線稱為懸鏈線．當(dāng)微積分尚未出現(xiàn)時(shí)，伽利略猜測(cè)這種形狀是拋物線，直到1691年萊布尼茲和伯努利借助微積分推導(dǎo)出懸鏈線的方程y=

  c

  2

  （

  e

  x

  c

  +

  e

  - x c

  ）

  ，其中c為參數(shù)．當(dāng)c=1時(shí)，函數(shù)

  cosh

  （

  x

  ）

  =

  e

  x

  +

  e

  -

  x

  2

  稱為雙曲余弦函數(shù)，與之對(duì)應(yīng)的函數(shù)

  sinh

  （

  x

  ）

  =

  e

  x

  -

  e

  -

  x

  2

  稱為雙曲正弦函數(shù)．關(guān)于雙曲函數(shù)，下列結(jié)論正確的是（　　）

  A．[sinh（x）]2-[cosh（x）]2=1	B．（cosh（x））'=-sinh（x）
  C．cosh（-1）＞cosh（2）	D．sinh（-x）=-sinh（x）
  組卷：79引用：1難度：0.7

  解析

• 7．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的左、右焦點(diǎn)分別為F₁，F(xiàn)₂，過(guò)F₁的直線與C的左支交于A、B兩點(diǎn)，且

  A

  F

  1

  =3

  F

  1

  B

  ，∠ABF₂=90°，則C的漸近線方程為（　　）

  A．y=±2x

  B． y =± 5 x

  C． y =± 6 2 x

  D． y =± 10 2 x
  組卷：183引用：2難度：0.6

  解析

四、解答題：本大題共6小題，共70分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.

• 21．某中學(xué)在2020年高考分?jǐn)?shù)公布后對(duì)高三年級(jí)各班的成績(jī)進(jìn)行分析．經(jīng)統(tǒng)計(jì)，某班有50名同學(xué)，總分都在區(qū)間[600，700]內(nèi)，將得分區(qū)間平均分成5組，統(tǒng)計(jì)頻數(shù)、頻率后，得到了如圖所示的“頻率分布”折線圖．
  
  （1）請(qǐng)根據(jù)頻率分布折線圖，畫(huà)出頻率分布直方圖，并根據(jù)頻率分布直方圖估計(jì)該班級(jí)的平均分；
  （2）經(jīng)過(guò)相關(guān)部門的計(jì)算，本次高考總分大于等于680的同學(xué)可以獲得高校T的“強(qiáng)基計(jì)劃”入圍資格．高校T的“強(qiáng)基計(jì)劃”校考分為兩輪．第一輪為筆試，所有入圍同學(xué)都要參加，考試科目為數(shù)學(xué)和物理，每科的筆試成績(jī)從高到低依次有A⁺，A，B，C四個(gè)等級(jí)，兩科中至少有一科得到A⁺，且兩科均不低于B，才能進(jìn)入第二輪，第二輪得到“通過(guò)”的同學(xué)將被高校T提前錄取．
  已知入圍的同學(xué)參加第一輪筆試時(shí)，總分高于690分的同學(xué)在每科筆試中取得A⁺，A，B，C的概率分別為

  2

  3

  ，

  1

  6

  ，

  1

  12

  ，

  1

  12

  ；總分不超過(guò)690分的同學(xué)在每科筆試中取得A⁺，A，B，C的概率分別為

  1

  3

  ，

  1

  4

  ，

  1

  6

  ，

  1

  4

  ；進(jìn)入第二輪的同學(xué)，若兩科筆試成績(jī)均為A⁺，則免面試，并被高校T提前錄取；若兩科筆試成績(jī)只有一個(gè)A⁺，則要參加面試，總分高于690分的同學(xué)面試“通過(guò)”的概率為

  2

  3

  ，總分不超過(guò)690分的同學(xué)面試“通過(guò)”的概率為

  2

  5

  ，面試“通過(guò)”的同學(xué)也將被高校T提前錄取．
  若該班級(jí)考分前10名都已經(jīng)報(bào)考了高校T的“強(qiáng)基計(jì)劃”，且恰有2人成績(jī)高于690分．求
  ①總分高于690分的某位同學(xué)沒(méi)有進(jìn)入第二輪的概率P₁；
  ②該班恰有兩名同學(xué)通過(guò)“強(qiáng)基計(jì)劃”被高校T提前錄取的概率P₂．
  組卷：216引用：5難度：0.7

  解析

• 22．對(duì)于正實(shí)數(shù)a,b（a＞b），熟知基本不等式：G（a,b）＜A（a,b），其中

  A

  （

  a

  ,

  b

  ）

  =

  a

  +

  b

  2

  為a,b的算術(shù)平均數(shù)，

  G

  （

  a

  ,

  b

  ）

  =

  ab

  為a,b的幾何平均數(shù)．現(xiàn)定義a,b的對(duì)數(shù)平均數(shù)：

  L

  （

  a

  ,

  b

  ）

  =

  a

  -

  b

  lna

  -

  lnb

  ．
  （Ⅰ）設(shè)x＞1，求證：

  lnx

  ＜

  1

  2

  （

  x

  -

  1

  x

  ）

  ；
  （Ⅱ）（ⅰ）利用第（Ⅰ）小問(wèn)證明不等式：G（a,b）＜L（a,b）；
  （ⅱ）若不等式k?L（a,b）＜G（a,b）+A（a,b）對(duì)于任意的正實(shí)數(shù)a,b（a＞b）恒成立，求正實(shí)數(shù)k的最大值．
  組卷：154引用：7難度：0.3

  解析