2022-2023學(xué)年湖南省株洲二中高一（上）月考數(shù)學(xué)試卷（A卷）（10月份）

一、單選題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設(shè)集合M={x∈Z||x-1|＜2}，N={y∈N|y=-x²+2x+1，x∈R}，則（　　）

  A．N∈M

  B．M?N

  C．N?M

  D．M=N
  組卷：62引用：2難度：0.7

  解析

• 2．設(shè)a,b∈R，則“ab+1=a+b”的充要條件是（　　）

  A．a(chǎn),b都為1	B．a(chǎn),b都不為1
  C．a(chǎn),b中至少有一個為1	D．a(chǎn),b都不為0
  組卷：62引用：5難度：0.8

  解析

• 3．設(shè)

  a

  =

  3

  -

  1

  2

  ，

  b

  =

  （

  1

  2

  ）

  -

  1

  3

  ，c=log₂

  1

  3

  ，則（　　）

  A．a(chǎn)＜c＜b

  B．c＜a＜b

  C．b＜c＜a

  D．a(chǎn)＜b＜c
  組卷：131引用：5難度：0.8

  解析

• 4．函數(shù)y=

  x

  a

  x

  |

  x

  |

  （

  a

  ＞

  1

  ）

  的圖象的大致形狀是（　　）

  A．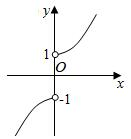

  B．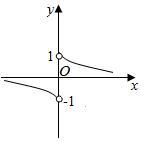

  C．

  D．
  組卷：3922引用：271難度：0.9

  解析

• 5．歷史上數(shù)學(xué)計算方面的三大發(fā)明分別是阿拉伯?dāng)?shù)字、十進制和對數(shù)，其中對數(shù)的發(fā)明，大大縮短了計算時間．對數(shù)運算對估算“天文數(shù)字”具有獨特優(yōu)勢，已知lg2≈0.301，lg5≈0.699，則2.5¹⁰的估算值為（　　）

  A．1000

  B．100000

  C．10000

  D．2500
  組卷：191引用：3難度：0.7

  解析

• 6．已知f（x）是奇函數(shù)，且在（0，+∞）上是增函數(shù)，又f（-2）=0，則

  f

  （

  x

  ）

  x

  -

  1

  ＜0的解集為（　　）

  A．（-2，0）∪（1，2）	B．（-2，0）∪（2，+∞）
  C．（-∞，-2）∪（1，2）	D．（-1，-2）∪（2，+∞）
  組卷：375引用：11難度：0.7

  解析

• 7．設(shè)x∈R，用[x]表示不超過x的最大整數(shù)，則y=[x]稱為高斯函數(shù)．例如：[π]=3，[-5，1]=-6，已知函數(shù)

  f

  （

  x

  ）

  =

  2

  x

  x

  2

  +

  1

  ，則函數(shù)y=[f（x）]的值域為（　　）

  A．{-1，1}

  B．{-1，0}

  C．{1，0}

  D．{-1，0，1}
  組卷：103引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說明，證明過程成演算步驟．

• 21．已知函數(shù)g（x）=ax²+c（a,c∈R），g（1）=1且不等式g（x）≤x²-x+1對一切實數(shù)x恒成立．
  （1）求函數(shù)g（x）的解析式；
  （2）設(shè)函數(shù)h（x）=2g（x）-2，關(guān)于x的不等式

  h

  （

  x

  -

  1

  ）

  +

  4

  h

  （

  m

  ）

  ≤

  h

  （

  x

  m

  ）

  -

  4

  m

  2

  h

  （

  x

  ）

  ．在

  x

  ∈

  [

  3

  2

  ，

  +

  ∞

  ）

  有解，求實數(shù)m的取值范圍．
  組卷：35引用：2難度：0.3

  解析

• 22．已知定義在R上的函數(shù)f（x）滿足f（-x）-f（x）=0且f（x）=log₂（2^x+1）+kx,g（x）=f（x）+x.
  （1）求f（x）的解析式；
  （2）若不等式g（4^x-a?2^x+1）＞g（-3）恒成立，求實數(shù)a取值范圍；
  （3）設(shè)h（x）=x²-2mx+1，若對任意的x₁∈[0，3]，存在x₂∈[1，3]，使得g（x₁）≥h（x₂），求實數(shù)m取值范圍．
  組卷：209引用：5難度：0.5

  解析