2023-2024學年江西省景德鎮市樂平中學高二（上）期中數學試卷

一、單項選擇題：（本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．已知點M（0，

  3

  ），點N（1，2

  3

  ），則直線MN的傾斜角為（　　）

  A．30°

  B．60°

  C．120°

  D．135°
  組卷：100引用：5難度：0.7

  解析

• 2．直線l：xcosα+ysinα=1（α∈R）與曲線C：x²+y²=1的交點個數為（　　）

  A．0

  B．1

  C．2

  D．無法確定
  組卷：119引用：2難度：0.8

  解析

• 3．動點P（x,y）滿足5

  （

  x

  -

  1

  ）

  2

  +

  （

  y

  -

  1

  ）

  2

  =|3x+4y-7|，則點P的軌跡是（　　）

  A．橢圓

  B．雙曲線

  C．拋物線

  D．直線
  組卷：40引用：2難度：0.7

  解析

• 4．已知雙曲線C：

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =1（a＞0，b＞0）的離心率為

  5

  2

  ，則C的漸近線方程為（　　）

  A．y=± 1 4 x

  B．y=± 1 3 x

  C．y=± 1 2 x

  D．y=±2x
  組卷：145引用：18難度：0.9

  解析

• 5．在空間直角坐標系中，已知A（1，0，1），B（1，1，-1），C（2，2，-1），則點B到直線AC的距離為（　　）

  A． 1 3

  B． 3 3

  C． 2 3

  D．1
  組卷：63引用：8難度：0.7

  解析

• 6．設P為直線3x-4y+11=0上的動點，過點P作圓C：x²+y²-2x-2y+1=0的兩條切線，切點分別為A，B，則四邊形PACB面積的最小值為（　　）

  A． 2

  B． 3

  C． 6

  D．2
  組卷：296引用：4難度：0.5

  解析

• 7．設F₁，F₂分別為橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點，點A，B均在C上，若

  F

  1

  A

  =2

  F

  2

  B

  ，2|F₁B|=5|F₁A|，則橢圓C的離心率為（　　）

  A． 2 2

  B． 5 3

  C． 6 4

  D． 10 5
  組卷：373引用：2難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．已知拋物線C：y²=2px（p＞0）的焦點F到雙曲線

  x

  2

  3

  -y²=1的漸近線的距離為

  1

  2

  ．
  （1）求拋物線C的方程；
  （2）過原點作兩條相互垂直的直線交曲線C于異于原點的兩點A，B，直線AB與x軸相交于N，試探究在x軸上是否存在異于N的定點M，使得x軸為∠AMB的角平分線，若存在，請求出M點坐標；若不存在，請說明理由．
  組卷：75引用：3難度：0.5

  解析

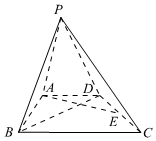• 22．已知四棱錐P-ABCD的底面ABCD是直角梯形，AD∥BC，AB⊥BC，AB=

  3

  ，BC=2AD=2，E為CD的中點，PB⊥AE
  （1）證明：平面PBD⊥平面ABCD；
  （2）若PB=PD，PC與平面ABCD所成的角為

  π

  4

  ，試問“在側面PCD內是否存在一點N，使得BN⊥平面PCD？”若存在，求出點N到平面ABCD的距離；若不存在，請說明理由．
  組卷：500引用：8難度：0.4

  解析