2022-2023學(xué)年山東省德州市慶云縣八年級（上）期中數(shù)學(xué)試卷
發(fā)布：2024/4/20 14:35:0
一、選擇題（本大題共12小題，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是正確的，把正確的選項(xiàng)選出來。每小題選對得4分，選錯、不選或選出的答案超過一個(gè)均記零分）
-
1．下列標(biāo)志是軸對稱圖形的是（ ）
組卷：156引用：8難度：0.8 -
2．下列長度的各組線段中，能作為一個(gè)三角形三邊的是（ ）
組卷：33引用：2難度：0.7 -
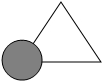3．如圖所示，亮亮?xí)系娜切伪荒E污染了一部分，很快他就根據(jù)所學(xué)知識畫出一個(gè)與書上完全一樣的三角形，那么這兩個(gè)三角形完全一樣的依據(jù)是（ ）組卷：2614引用：75難度：0.7 -
4．一副三角板按如圖所示的位置疊放在一起，則圖中∠α的度數(shù)是（ ）組卷：346引用：6難度：0.7 -
5．如圖，△ABC中，AD⊥BC于點(diǎn)D，CE⊥AB于點(diǎn)E，則AB邊上的高是（ ）組卷：219引用：4難度：0.7 -
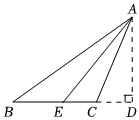6．如圖，在△ABC中，∠B=40°，∠ACB=110°，AE平分∠BAC，AD⊥BC交BC的延長線于點(diǎn)D，則∠DAE為（ ）組卷：46引用：2難度：0.7 -
7．如圖，△ABC中，AB=AE，且AD⊥BC，EF垂直平分AC，交AC于點(diǎn)F，交BC于點(diǎn)E，若△ABC周長為16，AC=6，則DC為（ ）組卷：5001引用：24難度：0.7 -
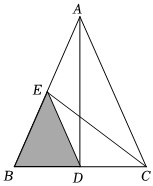8．如圖，在△ABC中，AB=AC，△ABC的面積為8，CE是AB邊上的中線，AD是底邊BC上的高，則圖中陰影部分的面積是（ ）組卷：51引用：2難度：0.6
三、解答題（本大題共7小題，共計(jì)78分．解答要寫出必要的文字說明、證明過程或演算步驟）
-
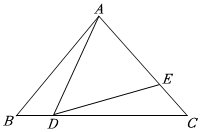24．如圖，在△ABC中，AB=AC，∠B=50°，點(diǎn)D在線段BC上運(yùn)動（不與點(diǎn)BC重合），連接AD，作∠ADE=50°，DE交線段AC于點(diǎn)E．
（1）當(dāng)∠BDA=110°時(shí)，求出∠BAD和∠DEC的度數(shù)；
（2）當(dāng)DC=AE時(shí)，△ABD和△DCE是否全等？請說明理由；
（3）在點(diǎn)D的運(yùn)動過程中，是否存在△ADE是等腰三角形的情形？若存在，請求出此時(shí)∠BDA的度數(shù)，若不存在，請說明理由．組卷：22引用：1難度：0.3 -
25．（1）如圖①：在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分別是BC、CD上的點(diǎn)，且EF=BE+FD，探究圖中∠BAE、∠FAD、∠EAF之間的數(shù)量關(guān)系．小王同學(xué)探究此問題的方法：延長FD到點(diǎn)G，使DG=BE，連接AG，先證明△ABE≌△ADG，再證△AEF≌△AGF，可得出∠EAF、∠BAE、∠FAD的數(shù)量關(guān)系是 ．
【靈活運(yùn)用】
（2）如圖②，若在四邊形ABCD中，AB=AD，∠B+∠D=180°，E、F分別是BC、CD上的點(diǎn)，且EF=BE+FD，上述結(jié)論是否仍然成立？請說明理由．
【延伸拓展】
（3）如圖③，在四邊形ABCD中，∠ABC+∠ADC=180°，AB=AD．若點(diǎn)E在CB的延長線上，點(diǎn)F在CD的延長線上，仍然滿足EF=BE+FD，請寫出∠EAF與∠DAB的數(shù)量關(guān)系，并給出證明過程．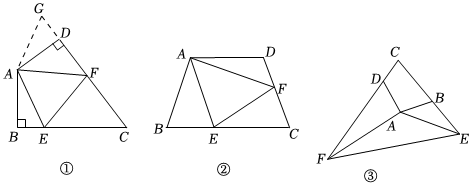
組卷：96引用：1難度：0.4