2022-2023學年吉林省長春二中高一（下）第一學程考試數學試卷

一、單選題（每題5分，共計40分）

• 1．已知向量

  a

  =

  （

  m

  ,

  2

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ）

  ，

  c

  =

  （

  1

  ，

  3

  ）

  ，且

  （

  2

  a

  -

  b

  ）

  ⊥

  c

  ，則實數m為（　　）

  A．-4

  B．-3

  C．4

  D．3
  組卷：544引用：9難度：0.8

  解析

• 2．已知向量

  a

  ，

  b

  滿足|

  a

  |=1，|

  b

  |=

  3

  ，|

  a

  -2

  b

  |=3，則

  a

  ?

  b

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：5557引用：32難度：0.7

  解析

• 3．對于任意的平面向量

  a

  ，

  b

  ，

  c

  ，下列說法中正確的是（　　）

  A．若 a ∥ b 且 b ∥ c ，則 a ∥ c

  B．若 a ? b = a ? c ，且 a ≠ 0 ，則 | b | = | c |

  C． （ a + b ） ? c = a ? c + b ? c

  D． （ a ? b ） c = a （ b ? c ）
  組卷：220引用：3難度：0.8

  解析

• 4．在△ABC中，若∠A=30°，b=1，

  S

  △

  ABC

  =

  3

  ，則

  a

  +

  b

  sin

  A

  +

  sin

  B

  的值為（　　）

  A． 2 13

  B． 2 37

  C． 37

  D． 13
  組卷：341引用：5難度：0.7

  解析

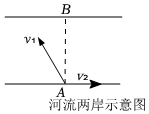• 5．長江流域內某地南北兩岸平行，如圖所示已知游船在靜水中的航行速度v₁的大小|v₁|=10km/h,水流的速度v₂的大小|v₂|=4km/h,設v₁和v₂所成角為θ（0＜θ＜π），若游船要從A航行到正北方向上位于北岸的碼頭B處，則cosθ等于（　　）

  A． - 21 5

  B． - 2 5

  C． - 3 5

  D． - 4 5
  組卷：89引用：4難度：0.7

  解析

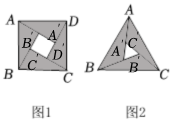• 6．東漢末年的數學家趙爽在《周髀算經》中利用一副“弦圖”給出了勾股定理的證明，后人稱其為“趙爽弦圖”．如圖1，它由四個全等的直角三角形與一個小正方形拼成的一個大正方形．我們通過類比得到圖2，它是由三個全等的鈍角三角形與一個小等邊三角形A′B′C′拼成的一個大等邊三角形ABC，若A'B'=2，cos∠ABB'=

  11

  14

  ，則AB=（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：150引用：6難度：0.7

  解析

• 7．在△ABC中，角A，B，C的對邊分別為a,b,c,已知（sinA+sinB）（a-b）=sinC（b+c），若角A的內角平分線AD的長為3，則b+c的最小值為（　　）

  A．12

  B．24

  C．27

  D．36
  組卷：502引用：6難度：0.5

  解析

四、解答題（17題10分，18—22題每題12分，共計70分）

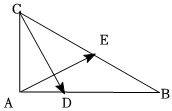• 21．如圖，在直角三角形ABC中，∠BAC=90°，CB=2CA=2．點D，E分別是線段AB，BC上的點，滿足

  AD

  =

  λ

  AB

  ，

  BE

  =

  λ

  BC

  ，

  λ

  ∈

  （

  0

  ，

  1

  ）

  ．
  （1）求

  AE

  ?

  BC

  的取值范圍；
  （2）是否存在實數λ，使得

  AE

  ⊥

  CD

  ？若存在，求出λ的值；若不存在，請說明理由．
  組卷：598引用：17難度：0.5

  解析

• 22．如圖，在平面四邊形ABCD中，AD=BD，∠ADB=90°．CD=2

  2

  ，BC=2．
  （1）若∠BDC=45°，求線段AC的長；
  （2）求線段AC長的最大值．
  組卷：270引用：11難度：0.6

  解析