2005年第十屆“華羅庚金杯”少年數學邀請賽決賽試卷（第2試）

一、解答題（共6題，每題10分，寫出解答過程）

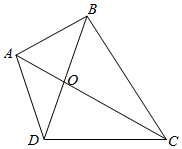• 1．如圖，四邊形ABCD中，對角線AC和BD交于O點．已知：AO=1，并且

  三角形

  ABD

  的面積

  三角形

  CBD

  的面積

  =

  3

  5

  ，那么OC的長是多少？
  組卷：67引用：1難度：0.9

  解析

• 2．將

  1

  2

  化成小數等于0.5，是個有限小數；將

  1

  11

  化成小數等于0.090…，簡記為

  0

  .

  ?

  0

  ?

  9

  ，是純循環小數；將

  1

  6

  化成小數等于0.1666…，簡記為

  0

  .

  1

  ?

  6

  ，是混循環小數．現在將2004個分數

  1

  2

  ，

  1

  3

  ，

  1

  4

  ，…，

  1

  2005

  化成小數，問：其中純循環小數有多少個？
  組卷：190引用：1難度：0.5

  解析

一、解答題（共6題，每題10分，寫出解答過程）

• 5．由26=1²+5²=1²+3²+4²，可以斷定26最多能表示為3個互不相等的非零自然數的平方和，請你判定360最多能表示為多少個互不相等的非零自然數的平方之和？
  組卷：85引用：1難度：0.3

  解析

• 6．有若干名小朋友，第一名小朋友的糖果比第二名小朋友的糖果多2塊，第二名小朋友的糖果比第三名小朋友的糖果多2塊，…，即前一名小朋友總比后一名小朋友多2塊糖果．他們按次序圍成圓圈做游戲，從第一名小朋友開始給第二名小朋友2塊糖果，第二名小朋友給第三名小朋友4塊糖果，…，即每一名小朋友總是將前面傳來的糖果再加上自己的2塊傳給下一名小朋友，當游戲進行到某一名小朋友收到上一名小朋友傳來的糖果但無法按規定給出糖果時，有兩名相鄰小朋友的糖果數的比是13：1，問最多有多少名小朋友？
  組卷：119引用：1難度：0.1

  解析