當前位置：試卷中心 > 試卷詳情

2022-2023學年貴州省六盤水二中高二（上）月考數學試卷（10月份）

發布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．若集合A={x|x＞1}，B={x|x²+3x＞0}．則A∩B=（　　）
A．{x|x＜-3} B．（x|x＜1} C．{x|x＞1} D．（x|x＞3}
組卷：24引用：3難度：0.8
解析
2．復數z滿足（3-4i²⁰²¹）?z=5i²⁰²²，則z在復平面內所對應的點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：25引用：2難度：0.8
解析
3．已知一直線經過點A（2，3，2），B（-1，0，5），下列向量中不是該直線的方向向量的為（　　）
A．
a
=
（
1
，
1
，
1
）
B．
a
=
（
-
1
，-
1
，
1
）
C．
a
=
（
-
3
，-
3
，
3
）
D．
a
=
（
1
，
1
，-
1
）
組卷：119引用：4難度：0.8
解析
4．已知點A（1，-2），B（m,2）且線段AB的垂直平分線的方程是x+2y-2=0，則實數m的值是（　　）
A．1 B．3 C．-2 D．-7
組卷：60引用：4難度：0.7
解析
5．已知向量
a
=（1，2），
b
=（1，0），
c
=（2，3），若λ為實數，（2
a
+λ
b
）⊥
c
，則λ=（　　）
A．8 B．-8 C．4 D．-4
組卷：85引用：3難度：0.7
解析
6．已知
sin
（
α
+
β
）
=
1
5
，
sin
（
α
-
β
）
=
3
5
，則
tanα
tanβ
的值為（　　）
A．．2 B．．-2 C．
1
2
D．．
-
1
2
組卷：218引用：10難度：0.9
解析
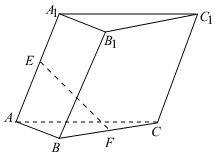7．已知斜三棱柱ABC-A₁B₁C₁所有棱長均為2，
∠
A
1
AB
=∠
A
1
AC
=
π
3
，點E、F滿足
AE
=
1
2
A
A
1
，
BF
=
1
2
BC
，則
|
EF
|
=（　　）
A．
6
B．
5
C．2 D．
2
組卷：814引用：14難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

21．對定義在[0，1]上，并且同時滿足以下兩個條件的函數f（x）稱為不等函數．
①對任意的x∈[0，1]，總有f（x）≥0；
②當x₁≥0，x₂≥0，x₁+x₂≤1時，總有f（x₁+x₂）≥f（x₁）+f（x₂）成立．
已知函數g（x）=x³與h（x）=2^x-a是定義在[0，1]上的函數．
（1）試問函數g（x）是否為不等函數？并說明理由；
（2）若函數h（x）是不等函數，求實數a組成的集合．
組卷：666引用：9難度：0.1
解析
22．如圖，點C在以AB為直徑的圓O上（C不同于A，B），PA垂直于圓O所在平面，G為△AOC的重心，PA=AB=2，N在線段PA上，且AN=2NP．
（1）證明：NG∥平面POC；
（2）在圓O上是否存在點C，使得二面角A-OP-G的余弦值為
2
3
？若存在，指出點C的位置；若不存在，說明理由．
組卷：92引用：3難度：0.5
解析