2022-2023學年山東省淄博五中八年級（上）期末數學試卷（五四學制）

一、單選題（每題4分，共40分）

• 1．已知，多項式x²-mx+n可因式分解為（x+3）（x-4），則m的值為（　　）

  A．-1

  B．1

  C．-7

  D．7
  組卷：351引用：4難度：0.6

  解析

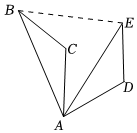• 2．如圖，將△ABC繞點A順時針旋轉60°得到△AED，若線段AB=5，則BE的長為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：347引用：7難度：0.7

  解析

• 3．在共有11人參加的演講比賽中，參賽選手的成績各不相同，因此選手要想知道自己是否進入前六名，只需了解自己的成績以及全部成績的（　　）

  A．平均數

  B．眾數

  C．中位數

  D．方差
  組卷：204引用：4難度：0.7

  解析

• 4．已知關于x的分式方程

  x

  x

  -

  2

  -3=

  k

  2

  -

  x

  的解為正數，則k的取值范圍是（　　）

  A．k＞-6

  B．k＞-2

  C．k＞-6且k≠-2

  D．k≥-6且k≠-2
  組卷：653引用：3難度：0.7

  解析

• 5．如圖所示的五邊形花環是用五個全等的等腰三角形拼成的，則∠BAC的度數為（　　）

  A．30°

  B．36°

  C．45°

  D．72°
  組卷：176引用：4難度：0.7

  解析

• 6．式子n²-1與n²+n的公因式是（　　）

  A．n+1

  B．n2

  C．n

  D．n-1
  組卷：1727引用：6難度：0.7

  解析

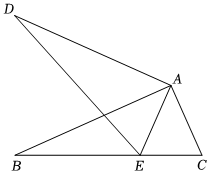• 7．如圖，△ABC繞點A，順時針旋轉48°，得到△ADE，點E落在BC邊上，連接BD，當BD⊥BC時，∠ABC的度數為（　　）

  A．24°

  B．42°

  C．48°

  D．66°
  組卷：172引用：2難度：0.6

  解析

三、解答題

• 22．（1）如圖①，△ABC與△ADE都是等腰直角三角形，且AB=AC，AD=AE，將△ADE繞點A旋轉到圖②的位置時，連接BD，CE相交于點P．
  ①求證：BD⊥CE．
  ②連接PA，猜想線段PA、PB、PC之間有怎樣的數量關系？并加以證明；
  （2）將△ADE繞點A旋轉到圖③的位置時，連接BD，CE相交于點P，連接PA，猜想線段PA、PB、PC之間有怎樣的數量關系？直接寫出結論，不需要證明．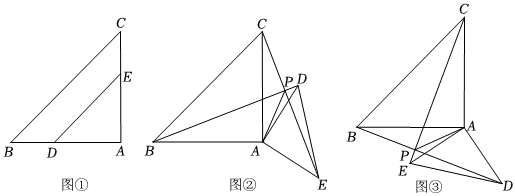
  
  組卷：813引用：3難度：0.1

  解析

• 23．如圖1，△ABC中，AB=AC，D為AB上一點，DE∥BC交AC于點E．
  
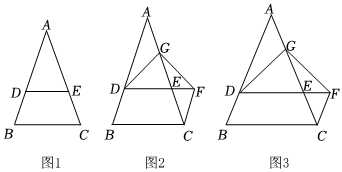
  （1）求證：BD=CE．
  （2）如圖2，過C作CF∥AB交DE延長線于F，G為AE上一點，AG=BD，連接DG、FG．求證：DG=FG．
  （3）如圖3，在（2）的條件下，若∠A=45°，∠DGC=∠B，EG=2，求AB的長．
  組卷：131引用：3難度：0.1

  解析