當前位置：試卷中心 > 試卷詳情

2011年浙江省金華市五中七年級（下）數學競賽試卷

發布：2024/4/20 14:35:0

1．已知：
20
n
是整數，則滿足條件的最小正整數n為（　　）
A．2 B．3 C．4 D．5
組卷：2022引用：58難度：0.9
解析
2．已知a+b=0，a≠b,則化簡
b
a
（
a
+
1
）
+
a
b
（
b
+
1
）
得（　　）
A．2a B．2b C．+2 D．-2
組卷：560引用：21難度：0.9
解析
3．若m+n=3，則2m²+4mn+2n²-6的值為（　　）
A．12 B．6 C．3 D．0
組卷：1103引用：76難度：0.9
解析
4．設△ABC的三邊長分別為a、b、c,其中a、b滿足|a+b-4|+（a-b+2）²=0，則第三邊的長c的取值范圍是（　　）
A．3＜c＜5 B．2＜c＜3 C．1＜c＜4 D．2＜c＜4
組卷：544引用：5難度：0.5
解析
5．如圖，有一塊直角三角板XYZ放置在△ABC上，恰好三角板XYZ的兩條直角邊XY、XZ分別經過點B，C，若∠A=35°，則∠ABX+∠ACX的度數是（　　）
A．25° B．35° C．45° D．55°
組卷：203引用：2難度：0.9
解析
6．從長度分別為1，3，5，7，9個單位的5條線段中任取3條作邊，能組成三角形的概率為（　　）
A．
1
5
B．
2
5
C．
1
2
D．
3
10
組卷：36引用：6難度：0.9
解析

17．上海世博會于2010年5月1日至2010年10月31日在上海舉行．
下表為世博會官方票務網站的幾種門票價格．李老師家用1600元作為購買門票的資金．

門票種類票價（元/張）

指定日普通票 200

平日普通票 160

夜票 100

（1）李老師若用全部資金購買“指定日普通票”和“夜票”共10張，則“指定日普通票”和“夜票”各買多少張？
（2）李老師若用全部資金購買“指定日普通票”、“平日普通票”和“夜票”共10張（每種至少一張），他的想法能實現嗎？請說明理由．
組卷：214引用：2難度：0.3
解析
18．已知四邊形ABCD中，∠A=∠C=90°，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN繞B點旋轉，它的兩邊分別交AD，DC（或它們的延長線）于E，F．
當∠MBN繞B點旋轉到AE=CF時（如圖1），易證AE+CF=EF；
當∠MBN繞B點旋轉到AE≠CF時，在圖2和圖3這兩種情況下，上述結論是否成立？若成立，請給予證明；若不成立，線段AE，CF，EF又有怎樣的數量關系？請寫出你的猜想，不需證明．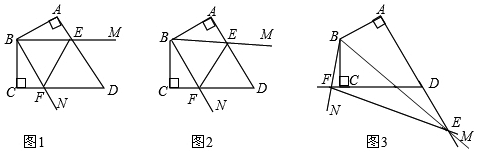
組卷：6635引用：37難度：0.1
解析