2022-2023學年安徽省安慶市宿松中學高二（下）期中數學試卷（A卷）

?一、單項選擇題。本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設集合A={x|1＜x≤2}，則?_RA=（　　）

  A．{x|x＜1或x≥2}

  B．{x|x＜1或x＞2}

  C．{x|x≤1或x≥2}

  D．{x|x≤1或x＞2}
  組卷：90引用：5難度：0.8

  解析

• 2．已知函數

  f

  （

  x

  ）

  =

  2 x 2 + 1 ， x ≤ 1

  2 x - 2 ， x ＞ 1

  ，則f（f（2））=（　　）

  A．5

  B．3

  C．2

  D．1
  組卷：94引用：4難度：0.8

  解析

• 3．已知向量

  a

  =

  （

  m

  ,

  1

  ，

  3

  ）

  ，

  b

  =

  （

  2

  ，

  n

  ,

  1

  ）

  ，若

  a

  ∥

  b

  ，則

  m

  n

  =（　　）

  A．2

  B．18

  C． 1 2

  D． 1 18
  組卷：438引用：4難度：0.8

  解析

• 4．已知等比數列{a_n}的公比q不為1，a₁=1，且a₂，a₄，a₃成等差數列，則q=（　　）

  A．1

  B．-1

  C． 1 2

  D． - 1 2
  組卷：51引用：3難度：0.7

  解析

• 5．《“健康中國2030”規劃綱要》提出，健康是促進人的全面發展的必然要求，是經濟社會發展的基礎條劃件．實現國民健康長壽，是國家富強、民族振興的重要標志，也是全國各族人民的共同愿望．為普及健康知識，某公益組織為社區居民組織了一場健康知識公益講座，為了解講座效果，隨機抽取了10位居民在講座后進行健康知識問卷（百分制），這十位居民的得分情況如表所示：
  

  答題居民序號	1	2	3	4	5	6	7	8	9	10
  得分	72	83	65	76	88	90	65	90	95	76

  則以下說法錯誤的是（　　）

  A．該10位居民的答卷得分的極差為30

  B．該10位居民的答卷得分的中位數為94

  C．該10位居民的答卷得分的中位數小于平均數

  D．該10位居民的答卷得分的方差為104.4
  組卷：16引用：3難度：0.7

  解析

• 6．已知函數

  f

  （

  x

  ）

  =

  1

  2

  sin

  2

  x

  +

  3

  2

  cos

  2

  x

  ，則將函數f（x）的圖象向右平移

  φ

  （

  0

  ＜

  φ

  ＜

  π

  2

  ）

  個單位后得到函數g（x）的圖象，g（x）圖象關于原點對稱，則（　　）

  A． φ = π 12

  B． φ = π 6

  C． φ = π 3

  D． φ = 5 π 12
  組卷：82引用：3難度：0.7

  解析

• 7．已知函數f（x）的定義域為R，且f（x+2）=2-f（2-x）+f（2），f（1）=-1，則f（3）=（　　）

  A．0

  B．2

  C．4

  D．5
  組卷：33引用：3難度：0.7

  解析

四、解答題。共70分解答應寫出文字說明、證明過程或演算步驟。

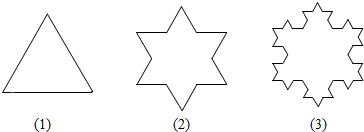
• 21．如圖（1）是一個邊長為1的正三角形，將每邊三等分，以中間一段為邊向外作正三角形，并擦去中間一段，得到圖（2），如此繼續下去，得到圖（3）…．由圖可知，圍成第一個圖形的線段條數為3，圍成第（2）個圖形的線段條數為12，?，設圍成第（n）個圖形的邊長條數為a_n．
  ?
  （1）求a₃，a₄，并直接寫出a_n（不用證明）；
  （2）數列{b_n}滿足

  n

  ∑

  i

  =

  1

  lo

  g

  4

  a

  i

  +

  1

  3

  b

  i

  =

  2

  n

  -

  1

  ，求數列{b_n}的前n項和．
  組卷：23引用：3難度：0.6

  解析

• 22．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點為F（4，0），P（-3，1）為雙曲線C上一點．
  （1）求C的方程；
  （2）設直線l：y=kx+m（k≠0），且不過點P，若l與C交于A，B兩點，點B關于原點的對稱點為D，若

  PA

  ?

  PD

  =

  0

  ，試判斷k是否為定值，若是，求出k值，若不是，請說明理由．
  組卷：138引用：4難度：0.3

  解析