2016-2017學年江蘇省泰州市泰興市黃橋中學八年級（上）第一次數學獨立作業

一、選擇題（共8小題，每小題2分，滿分16分）

• 1．下列圖形中不是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：731引用：23難度：0.9

  解析

• 2．在△ABC和△A′B′C′中，AB=A′B′，∠B=∠B′，補充條件后，仍不一定能保證△ABC≌△A′B′C′，這個補充條件是（　　）

  A．BC=B′C′

  B．∠A=∠A′

  C．AC=A′C′

  D．∠C=∠C′
  組卷：226引用：60難度：0.9

  解析

• 3．如圖，AC=AD，BC=BD，則有（　　）

  A．CD垂直平分AB	B．AB垂直平分CD
  C．AB與CD互相垂直平分	D．CD平分∠ACB
  組卷：336引用：17難度：0.9

  解析

• 4．到三角形三個頂點距離相等的是（　　）

  A．三邊高線的交點	B．三條中線的交點
  C．三條垂直平分線的交點	D．三條內角平分線的交點
  組卷：918引用：36難度：0.9

  解析

• 5．如圖，如果直線是多邊形的對稱軸，其中∠A=130°，∠B=110°，那么∠BCD的度數等于（　　）

  A．60°

  B．50°

  C．40°

  D．70°
  組卷：631引用：11難度：0.7

  解析

• 6．將一張菱形紙片，按圖（1）、（2）的方式沿虛線依次對折后．再沿圖（3）中的虛線裁剪得到圖（4），最后將圖（4）中的紙片打開鋪平，所得圖案應該是（　　）
  

  A．

  B．

  C．

  D．
  組卷：119引用：3難度：0.9

  解析

• 7．∠AOB的平分線上一點P到OA的距離為5，Q是OB上任一點，則（　　）

  A．PQ＞5

  B．PQ≥5

  C．PQ＜5

  D．PQ≤5
  組卷：939引用：42難度：0.9

  解析

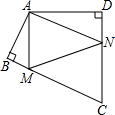• 8．四邊形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC、CD上分別找一點M、N，使三角形AMN周長最小時，則∠AMN+∠ANM的度數為（　　）

  A．80°

  B．90°

  C．100°

  D．130°
  組卷：2405引用：15難度：0.7

  解析

三、解答題（54分）

• 24．（1）觀察推理：如圖1，△ABC中，∠ACB=90°，AC=BC，直線l過點C，點A、B在直線l同側，BD⊥l,AE⊥l,垂足分別為D、E．
  求證：△AEC≌△CDB；
  （2）類比探究：如圖2，如圖，AB⊥MN，垂足為O，點P在射線OA上，點C在射線ON上，DP⊥PC且DP=PC，過點D作DE⊥OM于點E，則

  OC

  -

  DE

  OP

  的值為

  ．（直接寫答案）
  （3）拓展提升：如圖3，邊長為4cm正方形ABCD中，點E在DC上，且DE=1cm,動點F從點B沿射線BC以1cm/s速度向右運動，連接EF，將線段EF繞點E逆時針旋轉90°得到線段EH．要使點H恰好落在射線AD上，求點F運動的時間ts.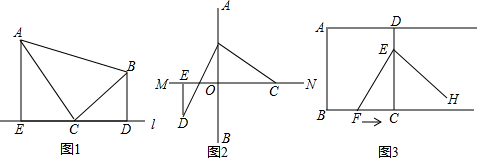
  
  組卷：362引用：1難度：0.3

  解析

• 25．問題背景：
  如圖1：在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分別是BC，CD上的點，且∠EAF=60°．探究圖中線段BE，EF，FD之間的數量關系．
  小王同學探究此問題的方法是，延長FD到點G．使DG=BE．連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論應是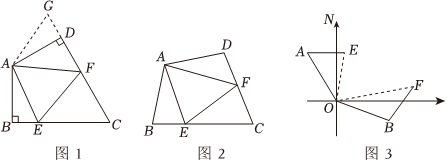

  ；
  
  探索延伸：
  如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°，E，F分別是BC，CD上的點，且∠EAF=

  1

  2

  ∠BAD，上述結論是否仍然成立，并說明理由；
  實際應用：
  如圖3，在某次軍事演習中，艦艇甲在指揮中心（O處）北偏西30°的A處，艦艇乙在指揮中心南偏東70°的B處，并且兩艦艇到指揮中心的距離相等，接到行動指令后，艦艇甲向正東方向以60海里/小時的速度前進，艦艇乙沿北偏東50°的方向以80海里/小時的速度前進，1.5小時后，指揮中心觀測到甲、乙兩艦艇分別到達E，F處，且兩艦艇之間的夾角為70°，試求此時兩艦艇之間的距離．
  組卷：2505引用：115難度：0.3

  解析