2023-2024學年廣東省廣州市越秀區執信中學高一（上）月考數學試卷（10月份）

一、單選題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．命題“?a∈R，ax²+1=0有實數解”的否定是（　?。?/h2>

  A．?a∈R，ax2+1≠0有實數解	B．?a∈R，ax2+1=0無實數解
  C．?a∈R，ax2+1=0無實數解	D．?a∈R，ax2+1≠0有實數解
  組卷：283引用：19難度：0.9

  解析

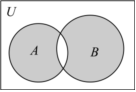• 2．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，則圖中陰影部分表示的集合為（　?。?br />?

  A．（-2，0]

  B．[-2，0]

  C．[-2，0]∪{4}

  D．（-2，0]∪{4}
  組卷：454引用：6難度：0.8

  解析

• 3．已知a＞b＞c＞0，則（　?。?/h2>

  A．2a＜b+c	B．a（b-c）＞b（a-c）
  C． 1 a - c ＞ 1 b - c	D．（a-c）3＞（b-c）3
  組卷：159難度：0.7

  解析

• 4．已知函數

  f

  （

  x

  ）

  =

  x 2 + x , x ＜ 0

  - x 2 ， x ≥ 0

  ，若f[f（a）]=2，則實數a的值為（　?。?/h2>

  A．-2

  B．1

  C． 2

  D．2
  組卷：50引用：2難度：0.5

  解析

• 5．已知命題p：a∈D，命題q：?x₀∈R，x₀²-ax₀-a≤-3，若p是q成立的必要不充分條件，則區間D為（　?。?/h2>

  A．（-∞，-6]∪[2，+∞）	B．（-∞，-4）∪（0，+∞）
  C．（-6，2）	D．[-4，0]
  組卷：203引用：7難度：0.6

  解析

• 6．若關于x的不等式（a²-4）x²+（a+2）x-1≥0的解集不為空集，則實數a的取值范圍為（　　）

  A．（-2， 6 5 ]	B．[-2， 6 5 ]
  C．（-∞，-2）∪[ 6 5 ，+∞）	D．（-∞，-2]∪[ 6 5 ，+∞）
  組卷：413難度：0.8

  解析

• 7．若對任意實數x＞0，y＞0，不等式

  x

  +

  xy

  ≤

  a

  （

  x

  +

  y

  ）

  恒成立，則實數a的最小值為（　?。?/h2>

  A． 2 - 1 2

  B． 2 - 1

  C． 2 + 1

  D． 2 + 1 2
  組卷：496難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知函數f（x）=x²+ax+2，a∈R．
  （1）若不等式f（x）≤0的解集為[1，2]，求不等式f（x）≥1-x²的解集；
  （2）若對于任意x∈[-1，1]，不等式f（x）≤2a（x-1）+4恒成立，求實數a的取值范圍；
  （3）已知g（x）=-x+m,當a=-3時，若對任意x₁∈[1，4]，總存在x₂∈（1，8），使f（x₁）=g（x₂）成立，求實數m的取值范圍．
  組卷：168引用：5難度：0.5

  解析

• 22．設函數

  f

  （

  x

  ）

  =

  1 a x , 0 ≤ x ≤ a

  1 1 - a （ 1 - x ） ， a ＜ x ≤ 1

  ，其中a為常數且a∈（0，1）．
  新定義：若x₀滿足f（f（x₀））=x₀，但f（x₀）≠x₀，則稱x₀為f（x）的回旋點．
  （1）當

  a

  =

  1

  2

  時，分別求

  f

  （

  f

  （

  1

  3

  ）

  ）

  和

  f

  （

  f

  （

  4

  5

  ）

  ）

  的值；
  （2）當x∈（a,1]時，求函數y=f（f（x））的解析式，并求出f（x）回旋點；
  （3）證明函數f（x）在x∈[0，1]有且僅有兩個回旋點，并求出回旋點x₁，x₂．
  組卷：110引用：2難度：0.2

  解析