2023-2024學年天津市第二南開中學高三（上）期中數學試卷

一、本卷共9小題，每小題5分，共45分.

• 1．設全集U={-3，-2，-1，0，1，2，3}，集合A={-1，0，1，2}，B={-3，0，2，3}，則A∩（?_UB）=（　　）

  A．{-3，3}	B．{0，2}
  C．{-1，1}	D．{-3，-2，-1，1，3 }
  組卷：4532引用：30難度：0.9

  解析

• 2．已知a,b∈R，則“a²=b²”是“a²+b²=2ab”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：3121引用：18難度：0.8

  解析

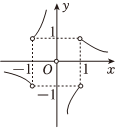• 3．已知函數y=f（x）的圖象如圖所示，則此函數的解析式可能是（　　）

  A． f （ x ） = | x 2 - 1 | x （ 1 - x 2 ）	B． f （ x ） = x 2 - 1 x | x 2 - 1 |
  C． f （ x ） = x 2 - 1 x 2 | x 2 - 1 |	D． f （ x ） = | x 2 - 1 | x 2 （ 1 - x 2 ）
  組卷：68引用：2難度：0.7

  解析

• 4．已知單位向量

  a

  ，

  b

  滿足|

  a

  +

  b

  |=1，則

  a

  在

  b

  方向上的投影向量為（　　）

  A． 1 2 b

  B．- 1 2 b

  C． 1 2 a

  D．- 1 2 a
  組卷：797引用：6難度：0.7

  解析

• 5．下列函數中，在區間（0，+∞）上單調遞增的是（　　）

  A．f（x）=-lnx

  B． f （ x ） = 1 2 x

  C． f （ x ） = - 1 x

  D．f（x）=3|x-1|
  組卷：1347引用：21難度：0.7

  解析

• 6．設a=3^0.7，

  b

  =

  （

  1

  3

  ）

  -

  0

  .

  8

  ，c=log_0.70.8，則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜a＜b
  組卷：926引用：20難度：0.7

  解析

三、解答題（本大題共5小題，共75分，解答應寫出文字說明，證明過程或演算步驟）

• 19．已知數列{a_n}是公差為2的等差數列，其前8項的和為64．數列{b_n}是公比大于0的等比數列，b₁=4，b₃-b₂=48．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）記c_n=b_2n+

  1

  b

  n

  ，n∈N*．
  （i）證明：{

  c

  2

  n

  -c_2n}是等比數列；
  （ii）證明：

  n

  ∑

  k

  =

  1

  a

  k

  a

  k

  +

  1

  c

  2

  k

  -

  c

  2

  k

  ＜2

  2

  （n∈N*）．
  組卷：4474引用：6難度：0.5

  解析

• 20．已知函數f（x）=x³+klnx（k∈R），f′（x）為f（x）的導函數．
  （Ⅰ）當k=6時，
  （ⅰ）求曲線y=f（x）在點（1，f（1））處的切線方程；
  （ⅱ）求函數g（x）=f（x）-f′（x）+

  9

  x

  的單調區間和極值；
  （Ⅱ）當k≥-3時，求證：對任意的x₁，x₂∈[1，+∞），且x₁＞x₂，有

  f

  ′

  （

  x

  1

  ）

  +

  f

  ′

  （

  x

  2

  ）

  2

  ＞

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ．
  組卷：5783引用：11難度：0.4

  解析