2021-2022學年廣東省深圳市寶安中學九年級（下）開學數學試卷

一．選擇題（每小題3分，共30分）

• 1．下列各數中，是無理數的是（　　）

  A．3. ? 1 ? 4

  B．π

  C． 3 8

  D． 9
  組卷：397引用：7難度：0.8

  解析

• 2．下列計算結果，正確的是（　　）

  A． （ - 3 ） 2 =-3

  B． 2 + 5 = 7

  C．2 3 - 3 =1

  D．（ 5 ）2=5
  組卷：1760引用：11難度：0.7

  解析

• 3．下列說法正確的是（　　）

  A．實數分為正實數和負實數

  B．負數沒有立方根

  C． 6 是最簡二次根式

  D．兩個無理數的和一定是無理數
  組卷：553引用：2難度：0.7

  解析

• 4．在一個不透明的口袋中，裝有若干個紅球和3個黃球，它們除顏色外沒有任何區別，搖勻后從中隨機摸出一個球，記下顏色后再放回口袋中，通過大量重復摸球試驗發現，摸到黃球的頻率是0.2，則估計盒子中紅球的個數大約是（　　）

  A．20個

  B．16個

  C．15個

  D．12個
  組卷：1350引用：3難度：0.5

  解析

• 5．下列命題是假命題的是（　　）

  A．四個角相等的四邊形是矩形

  B．對角線相等的平行四邊形是矩形

  C．對角線垂直的四邊形是菱形

  D．對角線垂直的平行四邊形是菱形
  組卷：1329引用：93難度：0.9

  解析

• 6．反比例函數y=

  k

  x

  與y=-kx+1（k≠0）在同一坐標系的圖象可能為（　　）

  A．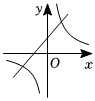

  B．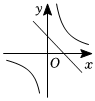

  C．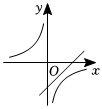

  D．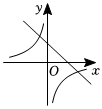
  組卷：9802引用：19難度：0.5

  解析

• 7．如圖，Rt△ABC中，∠BAC=90°，cosB=

  1

  4

  ，點D是邊BC的中點，以AD為底邊在其右側作等腰三角形ADE，使∠ADE=∠B，連結CE，則

  CE

  AD

  的值為（　　）

  A． 3 2

  B． 3

  C． 15 2

  D．2
  組卷：4340引用：9難度：0.4

  解析

三．解答題（共55分）

• 21．如圖，拋物線y=ax²+bx+c（a≠0），經過點A（-1，0），B（3，0），C（0，-3）三點．
  （1）求拋物線的解析式及頂點M的坐標；
  （2）連接AC、BC，N為拋物線上的點且在第一象限，當S_△NBC=S_△ABC時，求N點的坐標；
  （3）在（2）問的條件下，過點C作直線l∥x軸，動點P（m,-3）在直線l上，動點Q（m,0）在x軸上，連接PM、PQ、NQ，當m為何值時，PM+PQ+QN的和最小，并求出PM+PQ+QN和的最小值．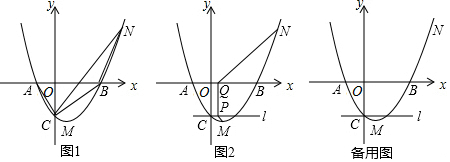
  
  組卷：1225引用：3難度：0.1

  解析

• 22．（1）證明推斷：如圖（1），在正方形ABCD中，點E、Q分別在邊BC、AB上，DQ⊥AE于點O，點G、F分別在邊CD、AB上，GF⊥AE．
  ①填空：DQ

  AE（填“＞”“＜”或“=”）；②推斷

  GF

  AE

  的值為

  ；
  （2）類比探究：如圖（2），在矩形ABCD中，

  BC

  AB

  =k（k為常數）．將矩形ABCD沿GF折疊，使點A落在BC邊上的點E處，得到四邊形FEPG，EP交CD于點H，連接AE交GF于點O．試探究GF與AE之間的數量關系，并說明理由；
  （3）拓展應用：在（2）的條件下，連接CP，當k=

  2

  3

  時，若

  BE

  BF

  =

  3

  4

  ，GF=2

  10

  ，求CP的長．
  
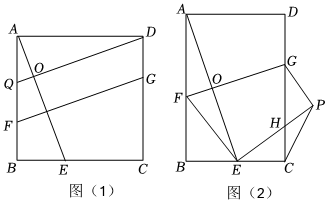  組卷：2362引用：5難度：0.1

  解析