當前位置：試卷中心 > 試卷詳情

2020-2021學年湖南省長沙市天心區明德中學高一（下）入學數學試卷

發布：2024/4/20 14:35:0

一、選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知全集U={1，2，3，4，5}，集合A={2，4}，B={3，4}，則A∪（?_UB）=（　　）
A．{2，3，4} B．{1，2，4，5} C．{2，5} D．{2}
組卷：132引用：5難度：0.9
解析
2．命題“?x≥0，sinx≤x”的否定是（　　）
A．．?x≥0，sinx＞x B．?x₀＜0，sinx₀＞x₀
C．?x₀≥0，sinx₀＞x₀ D．?x₀≥0，sinx₀≤x₀
組卷：65引用：6難度：0.9
解析
3．在同一直角坐標系中，
y
=
（
1
2
）
x
與y=log₂（-x）的圖象是（　　）
A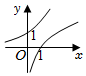． B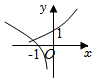． C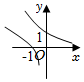． D．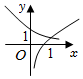
組卷：120引用：3難度：0.9
解析
4．函數f（x）=
2
x
+
ln
1
x
的零點所在的大致區間為（　　）
A．（1，2） B．（2，3）
C．（3，4） D．（1，2）與（2，3）
組卷：96引用：3難度：0.7
解析
5．已知a=sin160°，b=cos50°，c=tan110°，則a,b,c的大小關系為（　　）
A．a＜b＜c B．c＜b＜a C．c＜a＜b D．a＜c＜b
組卷：332引用：3難度：0.7
解析
6．已知f（x）是定義在R上的奇函數，且滿足f（x）=f（4-x），當x∈[0，2]時，f（x）=2^x-1，則f（21）=（　　）
A．-3 B．-1 C．1 D．3
組卷：383引用：3難度：0.7
解析
7．基本再生數R₀與世代間隔T是流行病學基本參數，基本再生數是指一個感染者傳染的平均人數，世代間隔指兩代間傳染所需的平均時間，在α型病毒疫情初始階段，可以用指數模型I（t）=e^rt描述累計感染病例數I（t）隨時間t（（單位：天）的變化規律，指數增長率r與R₀、T近似滿足R₀=1+rT，有學者基于已有數據估計出R₀=3.22，T=10．據此，在α型病毒疫情初始階段，累計感染病例數增加至I（0）的3倍需要的時間約為（　　）（參考數據：ln3≈1.10）
A．2天 B．3天 C．4天 D．5天
組卷：184引用：4難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

21．某企業參加A項目生產的工人為1000人，平均每人每年創造利潤10萬元．根據現實的需要，從A項目中調出x人參與B項目的售后服務工作，每人每年可以創造利潤10（a-
3
x
500
）萬元（a＞0），A項目余下的工人每年創造利潤需要提高0.2x%．
（1）若要保證A項目余下的工人創造的年總利潤不低于原來1000名工人創造的年總利潤，則最多調出多少人參加B項目從事售后服務工作？
（2）在（1）的條件下，當從A項目調出的人數不能超過總人數的40%時，才能使得A項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤，求實數a的取值范圍．
組卷：237引用：9難度：0.3
解析
22．已知函數
f
（
x
）
=
4
x
-
m
2
x
-
m
+
1
，函數
g
（
x
）
=
（
1
2
）
|
x
-
m
|
．
（1）若函數f（x）的圖象過點
（
1
，
1
2
）
，求m的值；
（2）在（1）的條件下，求函數h（x）=f（x）+g（x）在區間
[
1
2
，
4
3
]
上的最小值；
（3）若對?x₁∈[0，1]，都存在x₂∈[1，+∞），使得f（x₂）=g（x₁），求m的取值范圍．
組卷：186引用：2難度：0.1
解析