2021-2022學年四川省綿陽市南山中學高一（下）開學數學試卷

一、選擇題：本大題共12個小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設集合A={x|0＜x＜4），B={2，3，4}，則A∩B=（　　）

  A．{2，3}

  B．{1，2，3}

  C．{2，3，4}

  D．{1，2，3，4}
  組卷：44引用：4難度：0.9

  解析

• 2．已知弧長為π的扇形圓心角為

  π

  6

  ，則此扇形的面積為（　　）

  A．π

  B．2π

  C．3π

  D．4π
  組卷：270引用：3難度：0.8

  解析

• 3．在△ABC中，AB=5，AC=3，BC=7，則∠BAC=（　　）

  A． 5 π 6

  B． 2 π 3

  C． π 3

  D． π 6
  組卷：249引用：9難度：0.9

  解析

• 4．函數f（x）=tan（2x+

  π

  4

  ）的定義域為（　　）

  A．{x|x≠kπ+ π 2 ，k∈Z，x∈R}	B．{x|x≠2kπ+ π 2 ，k∈Z，x∈R}
  C．{x|x≠kπ+ π 8 ，k∈Z，x∈R}	D．{x|x≠ kπ 2 + π 8 ，k∈Z，x∈R}
  組卷：245引用：3難度：0.9

  解析

• 5．函數f（x）=e^x+2x-3的零點所在區間是（　　）

  A．（-2，-1）

  B．（-1，0）

  C．（1，2）

  D．（0，1）
  組卷：281引用：8難度：0.9

  解析

• 6．已知

  AB

  =（3，5），

  AC

  =（-1，2），則

  CB

  =（　　）

  A．（4，3）

  B．（-4，-3）

  C．（-4，3）

  D．（4，-3）
  組卷：527引用：7難度：0.8

  解析

• 7．函數f（x）=3^x+a與函數g（x）=log_ax（a＞0且a≠1）的圖象大致是（　　）

  A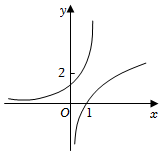．	B．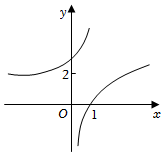
  C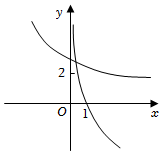．	D．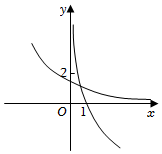
  組卷：83引用：6難度：0.9

  解析

三、解答題：本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知函數f（x）=2sin（ωx+φ）（ω＞0，

  |

  φ

  |

  ＜

  π

  2

  ），最小正周期T=π，

  f

  （

  0

  ）

  =

  3

  ．
  （1）求函數f（x）的解析式及函數f（x）的單調遞增區間；
  （2）函數y=f（x）-k在

  [

  0

  ，

  3

  π

  4

  ]

  上有兩個不同的零點x₁，x₂，求實數k的取值范圍．
  組卷：43引用：3難度：0.6

  解析

• 22．已知定義在R上的奇函數f（x）和偶函數g（x）滿足f（x）+g（x）=2^x．
  （1）求函數f（x）和g（x）的解析式；
  （2）判斷f（x）在R上的單調性，并用定義證明；
  （3）函數h（x）=f（|x²+8x+11|）+f（-k|x+1|）在R上恰有兩個零點，求實數k的取值范圍．
  組卷：77引用：3難度：0.5

  解析