2022-2023學年浙江省金蘭教育合作組織高二（上）期中數學試卷

一、選擇題：（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若點A（1，2），B（2，1），則直線AB的斜率是（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：56引用：2難度：0.9

  解析

• 2．圓x²+y²=1上的點到直線x+y-2=0距離的最小值是（　　）

  A． 2 - 1

  B．2

  C． 2 + 1

  D．4
  組卷：87引用：2難度：0.7

  解析

• 3．若方程

  x

  2

  2

  -

  k

  +

  y

  2

  k

  +

  2

  =

  1

  表示焦點在x軸上的橢圓，則實數k的取值范圍是（　　）

  A．（-∞，2）

  B．（-2，2）

  C．（-2，0）

  D．（0，2）
  組卷：591引用：9難度：0.8

  解析

• 4．在四面體OABC中記

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，若點M、N分別為棱OA、BC的中點，則

  MN

  =（　　）

  A． 1 2 a + 1 2 b + 1 2 c	B． - 1 2 a + 1 2 b + 1 2 c
  C． 1 2 a - 1 2 b + 1 2 c	D． 1 2 a + 1 2 b - 1 2 c
  組卷：644引用：17難度：0.7

  解析

• 5．圓C₁：x²+y²-4=0與圓C₂：x²+y²-4x+4y+4=0的公共弦的弦長等于（　　）

  A．2

  B．4

  C． 2

  D． 2 2
  組卷：287引用：13難度：0.8

  解析

• 6．設

  {

  a

  ，

  b

  ，

  c

  }

  為空間一組基底，若向量

  p

  =

  x

  a

  +

  y

  b

  +

  z

  c

  ，則向量

  p

  在基底

  {

  a

  ，

  b

  ，

  c

  }

  下的坐標為（x,y,z）．若

  q

  在基底

  {

  a

  ，

  b

  ，

  c

  }

  下的坐標為（2，3，4），則向量

  q

  在基底

  {

  a

  -

  b

  ，

  b

  -

  c

  ，

  c

  +

  a

  }

  下的坐標為（　　）

  A． （ - 5 2 ，- 1 2 ， 9 2 ）	B． （ 5 2 ，- 1 2 ， 9 2 ）
  C． （ - 5 2 ， 1 2 ， 9 2 ）	D． （ - 5 2 ， 1 2 ，- 9 2 ）
  組卷：129引用：2難度：0.6

  解析

• 7．PA，PB，PC是從點P出發的三條射線，每兩條射線夾角均為60°，則直線PC與平面PAB所成角的余弦值是（　　）

  A． 3 3

  B． 6 3

  C． 3 6

  D． 6 6
  組卷：347引用：5難度：0.5

  解析

四、解答題：（本題共6個小題，其中17題10分，18至22題每題12分，共70分.解答應寫出文字說明、證明過程或演算步聚）

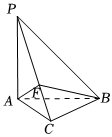• 21．在三棱錐P-ABC中，PA⊥平面ABC，PA=AB=2AC=2，∠BAC=60°，F為棱PC上一點，滿足AF⊥PC于F．
  （1）求證：平面ABF⊥平面PBC；
  （2）求PB與面ABF所成角的正弦值．
  組卷：97引用：2難度：0.7

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  經過點A（0，1），且離心率為

  6

  3

  ．
  （1）求橢圓C的方程；
  （2）橢圓C上的兩個動點M，N（M，N與點A不重合）直線AM，AN的斜率之和為4，作AH⊥MN于H．
  問：是否存在定點P，使得|PH|為定值．若存在，求出定點P的坐標及|PH|的值；若不存在，請說明理由．
  組卷：257引用：6難度：0.5

  解析