2022-2023學年浙江省杭州二中等四校聯盟高一（下）期中數學試卷

一、選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．請將你認為正確的答案填在答題卷的相應位置．

• 1．化簡

  PA

  -

  PB

  +

  AB

  所得的結果是（　　）

  A． 2 AB

  B． 2 BA

  C． 0

  D． PA
  組卷：227引用：4難度：0.8

  解析

• 2．已知m,n表示兩條不同的直線，α，β，γ表示三個不同的平面，則下列說法正確的是（　　）

  A．若m∥α，n∥α，則m∥n	B．若α⊥β，m⊥β，則m∥α
  C．若α⊥β，α⊥γ，則β∥γ	D．若m∥α，m⊥β，則α⊥β
  組卷：224引用：3難度：0.7

  解析

• 3．已知圓臺上、下底面的直徑分別為4和10，母線長為5，則該圓臺的體積為（　　）

  A． 145 π 3

  B． 116 π 3

  C．65π

  D．52π
  組卷：454引用：4難度：0.9

  解析

• 4．已知O是原點，點A（-2，4），B（1，a），若∠ABO為鈍角，則a的取值范圍是（　　）

  A．（1，2）	B．（-∞，1）∪（2，+∞）
  C．（1，3）	D．（-∞，1）∪（3，+∞）
  組卷：132引用：1難度：0.8

  解析

• 5．在△ABC中，角A，B，C所對的邊分別為a,b,c,則“acosB=c”是“△ABC是直角三角形”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：177引用：4難度：0.7

  解析

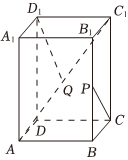• 6．已知長方體ABCD-A₁B₁C₁D₁的棱長AB=4，BC=3，AA₁=5，點P，Q分別是線段BB₁，AC₁上的動點（不包含端點），則下列說法正確的是（　　）

  A．對于任意一點Q，直線D1Q與直線BB1是異面直線

  B．對于任意一點Q，存在一點P，使得CP⊥D1Q

  C．對于任意一點P，存在一點Q，使得CP⊥D1Q

  D．以上說法都不正確
  組卷：97引用：1難度：0.6

  解析

• 7．在△ABC中，∠BAC=90°，AD是∠BAC的角平分線，AB=3，AC=4，E是AC的中點，則DE的長度為（　　）

  A． 2 37 7

  B． 2 17 7

  C． 37 7

  D． 17 7
  組卷：241引用：3難度：0.5

  解析

四、解答題：本大題共6小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

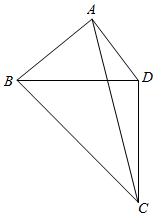• 21．為了美化環境，某公園欲將一塊空地規劃建成休閑草坪，休閑草坪的形狀為如圖所示的四邊形ABCD．其中AB=3百米，AD=

  5

  百米，且△BCD是以D為直角頂點的等腰直角三角形．擬修建兩條小路AC，BD（路的寬度忽略不計），設∠BAD=θ，θ∈（

  π

  2

  ，π）．
  （1）當cosθ=

  -

  5

  5

  時，求小路AC的長度；
  （2）當草坪ABCD的面積最大時，求此時小路BD的長度．
  組卷：748引用：19難度：0.4

  解析

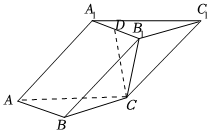• 22．如圖，在三棱柱ABC-A₁B₁C₁中，AB⊥AC，面ABC⊥面BCC₁B₁，且B₁C⊥AB，點D為棱A₁B₁的中點．
  （1）求證：直線B₁C⊥面ABC；
  （2）若AB=1，

  AC

  =

  3

  ，BB₁=3，求直線CD與面ABB₁A₁所成角的正弦值．
  組卷：265引用：1難度：0.5

  解析