2022-2023學(xué)年全國重點高中新百年競優(yōu)聯(lián)考高三（上）月考數(shù)學(xué)試卷（文科）（A）

一、選擇題（本大題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設(shè)集合A={-1，0，1，2，5}，B={x|x²-4x≤0}，則A∩B=（　　）

  A．{-1，0，5}

  B．{0，1，2}

  C．{-1，5}

  D．{1，2，5}
  組卷：1引用：1難度：0.7

  解析

• 2．已知命題p：?x∈R，x²+（a-1）x+1＜0．若命題p是假命題，則實數(shù)a的取值范圍為（　　）

  A．[1，3]

  B．[-1，3]

  C．（-1，3）

  D．[0，2]
  組卷：81引用：3難度：0.7

  解析

• 3．已知在△ABC中，

  DC

  =

  3

  BD

  ，若

  AB

  =

  m

  AC

  +

  n

  AD

  （m∈R，n∈R），則m-2n=（　　）

  A． 7 3

  B．-3

  C． 1 4

  D． - 5 4
  組卷：10引用：3難度：0.8

  解析

• 4．函數(shù)

  f

  （

  x

  ）

  =

  ln

  （

  x

  2

  +

  1

  -

  x

  ）

  +x²sinx+5在[-π，π]上的最大值與最小值的和為（　　）

  A．-10

  B．2

  C．10

  D．不確定
  組卷：8引用：1難度：0.7

  解析

• 5．已知x²+ax+b≤0的解集是{x|x=c}，若x²+ax+b＜d的解集為（x₁，x₂），|x₁-x₂|=

  2

  6

  ，則d=（　　）

  A．24

  B．12

  C．6

  D． 6
  組卷：19引用：1難度：0.7

  解析

• 6．已知數(shù)列{a_n}滿足a₁=2，且

  （

  n

  +

  1

  ）

  a

  n

  +

  1

  -

  n

  a

  n

  =

  2

  n

  ，則a₄=（　　）

  A．2

  B．4

  C．6

  D．8
  組卷：140引用：4難度：0.7

  解析

• 7．已知點P（4，3）是角α的終邊上一點，則

  tan

  α

  2

  =（　　）

  A． 1 3

  B． ± 1 3

  C．3或 1 3

  D．3
  組卷：70引用：5難度：0.7

  解析

三、解答題（共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟

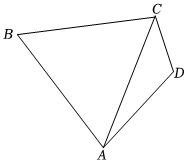• 21．如圖所示，在平面四邊形ABCD中，

  co

  s

  2

  （

  π

  2

  +

  B

  ）

  +

  cos

  B

  =

  5

  4

  ，AB=AC，AD=2CD=4．
  （1）求角B的大小；
  （2）當(dāng)角D為何值時，四邊形ABCD的面積最大．
  組卷：20引用：2難度：0.5

  解析

• 22．已知函數(shù)f（x）=xlnx-ax²-x+a,（a∈R）．
  （1）當(dāng)a=1時，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）若函數(shù)f（x）有兩個不同的極值點x₁，x₂（其中x₁＜x₂），證明：x₁?

  x

  2

  2

  ＞e³．
  組卷：26引用：1難度：0.6

  解析