2022-2023學(xué)年遼寧省沈陽市五校協(xié)作體高二（下）期中數(shù)學(xué)試卷

一、單選題

• 1．等差數(shù)列{a_n}的前n項和為S_n，若a₂=1，a₃=3，則S₄=（　　）

  A．12

  B．10

  C．8

  D．6
  組卷：451引用：35難度：0.9

  解析

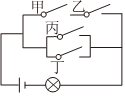• 2．如圖，已知電路中4個開關(guān)閉合的概率都是

  1

  2

  ，且是相互獨立的，則燈亮的概率為（　　）

  A． 1 16

  B． 3 16

  C． 1 4

  D． 13 16
  組卷：202引用：6難度：0.7

  解析

• 3．現(xiàn)有17匹善于奔馳的馬，它們從同一個起點出發(fā)，測試它們一日可行的路程．已知第i（i=1，2，…，16）匹馬的日行路程是第i+1匹馬日行路程的1.05倍，且第16匹馬的日行路程為315里，則這17匹馬的日行路程之和約為（取1.05¹⁷=2.292）（　　）

  A．7750里

  B．7752里

  C．7754里

  D．7756里
  組卷：66引用：3難度：0.8

  解析

• 4．口袋中有相同的黑色小球n個，紅、白、藍(lán)色的小球各一個，從中任取4個小球．ξ表示當(dāng)n=3時取出黑球的數(shù)目，η表示當(dāng)n=4時取出黑球的數(shù)目．則下列結(jié)論成立的是（　　）

  A．E（ξ）＜E（η），D（ξ）＜D（η）	B．E（ξ）＞E（η），D（ξ）＜D（η）
  C．E（ξ）＜E（η），D（ξ）＞D（η）	D．E（ξ）＞E（η），D（ξ）＞D（η）
  組卷：433引用：4難度：0.4

  解析

• 5．已知函數(shù)f（x）=nx+lnx（n∈N^*）的圖象在點

  （

  1

  n

  ，

  f

  （

  1

  n

  ）

  ）

  處的切線的斜率為a_n，則數(shù)列

  {

  1

  a

  n

  a

  n

  +

  1

  }

  的前n項和S_n為（　　）

  A． 1 n + 1	B． 3 n 2 + 5 n 2 （ n + 1 ） （ n + 2 ）
  C． n 4 （ n + 1 ）	D． 3 n 2 + 5 n 8 （ n + 1 ） （ n + 2 ）
  組卷：170引用：7難度：0.7

  解析

• 6．32名業(yè)余棋手組隊與甲、乙2名專業(yè)棋手進(jìn)行車輪挑戰(zhàn)賽，每名業(yè)余棋手隨機選擇一名專業(yè)棋手進(jìn)行一盤比賽，每盤比賽結(jié)果相互獨立，若獲勝的業(yè)余棋手人數(shù)不少于10名，則業(yè)余棋手隊獲勝．已知每名業(yè)余棋手與甲比賽獲勝的概率均為

  1

  3

  ，每名業(yè)余棋手與乙比賽獲勝的概率均為

  1

  4

  ，若業(yè)余棋手隊獲勝，則選擇與甲進(jìn)行比賽的業(yè)余棋手人數(shù)至少為（　　）

  A．24

  B．25

  C．26

  D．27
  組卷：156引用：3難度：0.7

  解析

• 7．已知函數(shù)f（x）與g（x）定義域都為R，滿足

  f

  （

  x

  ）

  =

  （

  x

  +

  1

  ）

  g

  （

  x

  ）

  e

  x

  ，且有g(shù)'（x）+xg'（x）-xg（x）＜0，g（1）=2e,則不等式f（x）＜4的解集為（　　）

  A．（1，4）

  B．（0，2）

  C．（-∞，2）

  D．（1，+∞）
  組卷：185引用：3難度：0.5

  解析

四、解答題

• 21．已知函數(shù)f（x）=lnx-

  1

  2

  a

  x

  2

  +x（a＞0）．
  （1）若a=1，求函數(shù)f（x）在點（1，f（1））處的切線方程；
  （2）若函數(shù)f（x）=lnx-

  1

  2

  a

  x

  2

  +x（a＞0）在其定義域上有唯一零點，求實數(shù)a的值．
  組卷：176引用：4難度：0.6

  解析

• 22．馬爾可夫鏈?zhǔn)且蚨韲鴶?shù)學(xué)家安德烈?馬爾可夫得名，其過程具備“無記憶”的性質(zhì)，即第n+1次狀態(tài)的概率分布只跟第n次的狀態(tài)有關(guān)，與第n-1，n-2，n-3，…次狀態(tài)是“沒有任何關(guān)系的”．現(xiàn)有甲、乙兩個盒子，盒子中都有大小、形狀、質(zhì)地相同的2個紅球和1個黑球．從兩個盒子中各任取一個球交換，重復(fù)進(jìn)行n（n∈N^*）次操作后，記甲盒子中黑球個數(shù)為X_n，甲盒中恰有1個黑球的概率為a_n，恰有2個黑球的概率為b_n．
  （1）求X₁的分布列；
  （2）求數(shù)列{a_n}的通項公式；
  （3）求X_n的期望．
  組卷：1418引用：5難度：0.3

  解析