2022-2023學年福建省泉州市晉江市季延中學高二（上）期中數學試卷

一、單選題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．在空間直角坐標系中，點A（6，-6，6）關于xOz平面對稱點的坐標是（　　）

  A．（-6，6，6）

  B．（6，6，6）

  C．（6，6，-6）

  D．（-6，6，-6）
  組卷：53引用：4難度：0.8

  解析

• 2．直線ax+y-a=0（a∈R）與圓（x-2）²+y²=4的位置關系是（　　）

  A．相離

  B．相交

  C．相切

  D．無法確定
  組卷：116引用：7難度：0.7

  解析

• 3．曲線

  x

  2

  5

  +

  y

  2

  9

  =

  1

  與曲線

  x

  2

  5

  -

  k

  +

  y

  2

  9

  -

  k

  =

  1

  （

  k

  ＜

  5

  ）

  的（　　）

  A．長軸長相等

  B．短軸長相等

  C．離心率相等

  D．焦距相等
  組卷：79引用：1難度：0.6

  解析

• 4．已知向量

  {

  a

  ，

  b

  ，

  c

  }

  是空間的一個基底，向量

  {

  a

  -

  b

  ，

  a

  +

  b

  ，

  c

  }

  是空間的另一個基底，一向量

  p

  在基底

  {

  a

  ，

  b

  ，

  c

  }

  下的坐標為（2，1，-1），則向量

  p

  在基底

  {

  a

  -

  b

  ，

  a

  +

  b

  ，

  c

  }

  下的坐標為（　　）

  A． （ 1 2 ， 3 2 ，- 1 ）	B． （ 3 2 ，- 1 2 ，- 1 ）
  C． （ 1 2 ， 3 2 ， 1 ）	D． （ - 1 2 ，- 3 2 ，- 1 ）
  組卷：359引用：6難度：0.8

  解析

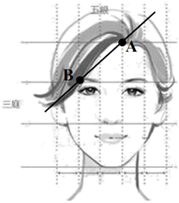• 5．美術繪圖中常采用“三庭五眼”作圖法．三庭：將整個臉部按照發際線至眉骨，眉骨至鼻底，鼻底至下頦的范圍分為上庭、中庭、下庭，各占臉長的

  1

  3

  ，五眼：指臉的寬度比例，以眼形長度為單位，把臉的寬度自左至右分成第一眼、第二眼、第三眼、第四眼、第五眼五等份．如圖，假設三庭中一庭的高度為2cm,五眼中一眼的寬度為1cm,如圖中提供的直線AB近似記為該人像的劉海邊緣，且該人像的鼻尖位于中庭下邊界和第三眼的中點，則該人像鼻尖到劉海邊緣的距離約為（　　）

  A．1.8cm

  B．2.5cm

  C．3.2cm

  D．3.9cm
  組卷：109引用：9難度：0.7

  解析

• 6．橢圓

  x

  2

  9

  +

  y

  2

  2

  =

  1

  的左、右焦點分別為F₁、F₂，動點A在橢圓上，B為橢圓的上頂點，則△ABF₂周長的最大值為（　　）

  A．8

  B．10

  C．12

  D．16
  組卷：190引用：4難度：0.5

  解析

• 7．已知點P在直線y=x-2上運動，點E是圓x²+y²=1上的動點，點F是圓（x-6）²+（y+2）²=9上的動點，則|PF|-|PE|的最大值為（　　）

  A．6

  B．7

  C．8

  D．9
  組卷：242引用：6難度：0.5

  解析

四、解答題（共70分．解答應寫出文字說明、證明過程或演算步驟．）

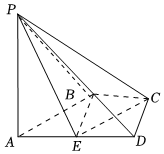• 21．如圖，在四棱錐P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=

  1

  2

  AD=1，E為邊AD的中點，異面直線PA與CD所成的角為90°．
  （1）在直線PA上找一點M，使得直線CM∥平面PBE，并求

  AM

  AP

  的值；
  （2）若直線CD到平面PBE的距離為

  2

  5

  5

  ，求平面PBE與平面PBC夾角的正弦值．
  組卷：257引用：6難度：0.6

  解析

• 22．已知橢圓C的中心為O，離心率為

  2

  2

  ．圓O在C的內部，半徑為

  6

  3

  ．P，Q分別為C和圓O上的動點，且P，Q兩點的最小距離為

  1

  -

  6

  3

  ．
  （1）建立適當的坐標系，求C的方程；
  （2）A，B是C上不同的兩點，且直線AB與以OA為直徑的圓的一個交點在圓O上．求證：以AB為直徑的圓過定點．
  組卷：857引用：2難度：0.3

  解析