2022-2023學年重慶市長壽中學高二（上）期末數學試卷

一．單選題：本小題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的，答案請涂寫在機讀卡上

• 1．已知直線l過A（-1，1）、B（1，3）兩點，則直線l的傾斜角的大小為（　　）

  A． π 4

  B． π 3

  C． 2 π 3

  D． 3 π 4
  組卷：199引用：8難度：0.8

  解析

• 2．已知圓

  C

  1

  ：

  （

  x

  -

  2

  ）

  2

  +

  （

  y

  -

  3

  ）

  2

  =

  1

  和圓

  C

  2

  ：

  （

  x

  -

  3

  ）

  2

  +

  （

  y

  -

  4

  ）

  2

  =

  16

  ，則圓C₁與圓C₂的位置關系為（　　）

  A．內含

  B．外切

  C．相交

  D．相離
  組卷：181引用：2難度：0.8

  解析

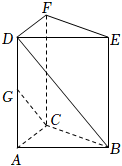• 3．三棱柱ABC-DEF中，G為棱AD的中點，若

  BA

  =

  a

  ，

  BC

  =

  b

  ，

  BD

  =

  c

  ，則

  CG

  =（　　）

  A． - a + b - c

  B． 1 2 a - b + 1 2 c

  C． - 1 2 a + b + c

  D． - 1 2 a + 1 2 b + c
  組卷：1436引用：31難度：0.7

  解析

• 4．雙曲線C：

  y

  2

  25

  -

  x

  2

  39

  =1上的點P到上焦點的距離為12，則P到下焦點的距離為（　　）

  A．22

  B．2

  C．2或22

  D．24
  組卷：472引用：10難度：0.8

  解析

• 5．設等差數列{a_n}的前n項和為S_n，若S₃=16，S₆=8，則S₁₂=（　　）

  A．-50

  B．-60

  C．-70

  D．-80
  組卷：399引用：5難度：0.7

  解析

• 6．已知點P是圓C：x²+y²-2x-4y+3=0的動點，直線l：x-y-3=0上存在兩點A，B，使得∠APB≥

  π

  2

  恒成立，則線段AB長度的最小值是（　　）

  A．6 2

  B．2 2

  C．4 2

  D．4 2 +1
  組卷：334引用：7難度：0.5

  解析

• 7．設拋物線C：y²=2px（p＞0）的焦點是F，直線l與拋物線C相交于P，Q兩點，且

  ∠

  PFQ

  =

  2

  π

  3

  ，線段PQ的中點A到拋物線C的準線的距離為d,則

  （

  |

  PQ

  |

  d

  ）

  2

  的最小值為（　　）

  A． 3

  B． 3 3

  C．3

  D． 1 3
  組卷：448引用：7難度：0.5

  解析

四．解答題（本大題共6個小題，共70分．解答應寫出必要的文字說明、證明

• 21．拋物線C：y²=2px（p＞0），拋物線的焦點是雙曲線x²-2y²=1的右頂點，過點Q（1，3）作直線與C交于M，N兩點．
  （1）求C的方程．
  （2）若C的一條弦ST經過C的焦點，且直線ST與直線MN平行，試問是否存在常數λ，使得|QM|?|QN|=λ|SF|?|TF|成立？若存在，求λ的值；若不存在，請說明理由．
  組卷：67引用：3難度：0.4

  解析

• 22．已知點A（0，2）與B（0，-2），動點M（x,y）滿足直線AM，BM的斜率之積為

  -

  1

  2

  ，則點M的軌跡為曲線C．
  （1）求曲線C的方程；
  （2）若點T在直線y=3上，直線TA，TB分別與曲線C交于點E，F，求△TAB與△TEF面積之比的最大值．
  組卷：283引用：4難度：0.4

  解析