2020-2021學(xué)年江蘇省揚(yáng)州市廣陵區(qū)樹(shù)人學(xué)校九年級(jí)（下）周測(cè)數(shù)學(xué)試卷

一、選擇題

• 1．下列四個(gè)數(shù)中，最大的實(shí)數(shù)是（　　）

  A．-2021

  B．1

  C．-1

  D．2021
  組卷：20引用：2難度：0.8

  解析

• 2．下列計(jì)算正確的是（　　）

  A．（a3）2=a5

  B．a(chǎn)3?a5=a8

  C．a(chǎn)5+a2=a7

  D．a(chǎn)6÷a2=a3
  組卷：185引用：7難度：0.8

  解析

• 3．若代數(shù)式

  x

  +

  1

  有意義，則實(shí)數(shù)x的取值范圍是（　　）

  A．x≥1

  B．x≤1

  C．x≥-1

  D．x≤-1
  組卷：257引用：2難度：0.8

  解析

• 4．已知m是一元二次方程x²-x-2=0的一個(gè)根，則2021-m²+m的值為（　　）

  A．2020

  B．2019

  C．2018

  D．2017
  組卷：571引用：4難度：0.6

  解析

• 5．曲橋是我國(guó)古代經(jīng)典建筑之一，它的修建增加了游人在橋上行走的路程，有利于游人更好地觀賞風(fēng)光．如圖，A、B兩地間修建曲橋與修建直的橋相比，增加了橋的長(zhǎng)度，其中蘊(yùn)含的數(shù)學(xué)道理是（　　）

  A．兩點(diǎn)之間，線段最短

  B．平行于同一條直線的兩條直線平行

  C．垂線段最短

  D．兩點(diǎn)確定一條直線
  組卷：1888引用：34難度：0.8

  解析

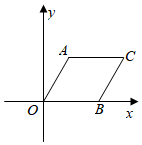• 6．如圖，菱形AOBC的邊BO在x軸正半軸上，點(diǎn)A（2，2

  3

  ），反比例函數(shù)y=

  k

  x

  的圖象經(jīng)過(guò)點(diǎn)C，則k的值為（　　）

  A．12

  B． 4 3

  C． 12 3

  D． 6 3
  組卷：377引用：5難度：0.6

  解析

• 7．關(guān)于x的方程x²+ax+b=0，有下列四個(gè)命題：
  甲：x=1是該方程的根
  乙：該方程兩根之和為2
  丙：x=3是該方程的根
  丁：該方程兩根異號(hào)
  如果有一個(gè)命題是假命題，則該命題是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：20引用：4難度：0.5

  解析

三、解答題

• 21．在平面直角坐標(biāo)系中，點(diǎn)A的坐標(biāo)為（a,b），若點(diǎn)A₁的坐標(biāo)是（a,|a-b|），則稱點(diǎn)A₁是點(diǎn)A的“關(guān)聯(lián)點(diǎn)”．
  （1）點(diǎn)（-1，3）的“關(guān)聯(lián)點(diǎn)”坐標(biāo)是

  ；
  （2）點(diǎn)A在函數(shù)y=2x-3上，若點(diǎn)A的“關(guān)聯(lián)點(diǎn)”A₁與點(diǎn)A重合，求點(diǎn)A的坐標(biāo)；
  （3）點(diǎn)A（a,b）的“關(guān)聯(lián)點(diǎn)”A₁是函數(shù)y=x²的圖象上一點(diǎn)，當(dāng)0≤a≤2時(shí)，求線段AA₁長(zhǎng)度的最大值．
  組卷：174引用：2難度：0.1

  解析

• 22．閱讀感悟：
  “數(shù)形結(jié)合”是一種重要的數(shù)學(xué)思想方法，同一個(gè)問(wèn)題有“數(shù)”、“形”兩方面的特性，解決數(shù)學(xué)問(wèn)題，有的從“數(shù)”入手簡(jiǎn)單，有的從“形”入手簡(jiǎn)單，因此，可能“數(shù)”→“形”或“形”→“數(shù)”，有的問(wèn)題需要經(jīng)過(guò)幾次轉(zhuǎn)化．這對(duì)于初、高中數(shù)學(xué)的解題都很有效，應(yīng)用廣泛．
  解決問(wèn)題：
  （1）如圖1，?ABCD，AB=15，AD=14，AC=13，求tanB；
  （2）已知函數(shù)y₁=x²，y₂=ax-1，當(dāng)x＜

  1

  2

  時(shí)，y₁＞y₂，則整數(shù)a可取的最大值與最小值的和是

  ；
  （3）如圖2，矩形ABCD的邊長(zhǎng)AB=2，BC=3，點(diǎn)E、F分別是AD、BC邊上的動(dòng)點(diǎn)（與矩形頂點(diǎn)不重合），連接BE、CE，過(guò)F作FG∥CE交BE于G，作FH∥BE交CE于H．當(dāng)△EFG面積最大時(shí)，求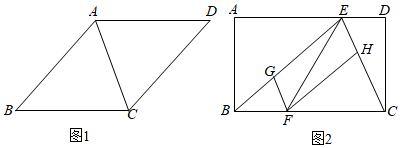

  EH

  CH

  的值．
  
  組卷：282引用：2難度：0.2

  解析