2023-2024學年北京市朝陽區陳經綸中學高三（上）診斷數學試卷（9月份）

一、選擇題（本題共10題，每小題4分，滿分40分）

• 1．設全集為R，若集合A={x|x²＜4}，B={x|log₂x＞0}，則A∩（?_RB）=（　　）

  A．{x|1＜x＜2}

  B．{x|-2＜x≤1}

  C．{x|1≤x＜2}

  D．{x|-2＜x＜1}
  組卷：87引用：4難度：0.8

  解析

• 2．設復數z滿足

  z

  1

  -

  i

  =

  1

  +

  2

  i

  ，則它的共軛復數

  z

  的虛部為（　　）

  A．-1

  B．1

  C．-i

  D．i
  組卷：48引用：2難度：0.7

  解析

• 3．下列函數中，是奇函數且在定義域內單調遞減的是（　　）

  A．f（x）=sinx	B．f（x）=2|x|
  C．f（x）= 2 x	D．f（x）= 1 2 （ e - x - e x ）
  組卷：27引用：5難度：0.7

  解析

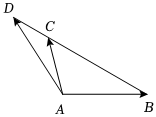• 4．如圖所示，點C在線段BD上，且BC=3CD，則

  AD

  =（　　）

  A． 3 AC - 2 AB

  B． 4 AC - 3 AB

  C． 4 3 AC - 1 3 AB

  D． 1 3 AC - 2 3 AB
  組卷：124引用：6難度：0.7

  解析

• 5．已知直線m,直線n和平面α，則下列四個命題中正確的是（　　）

  A．若m∥α，n?α，則m∥n	B．若m∥α，n∥α，則m∥n
  C．若m⊥α，n∥α，則m⊥n	D．若m⊥n,n∥α，則m⊥α
  組卷：602引用：6難度：0.7

  解析

• 6．若a,b為實數，且0＜ab＜1，則以下結論中正確的是（　　）

  A． a ＜ 1 b

  B．a＞0，b＞0

  C．0＜a3b2＜1

  D． - 1 ab ＜ - 1
  組卷：119引用：4難度：0.7

  解析

• 7．函數f（x）=cos2x+6cos（

  π

  2

  -x）（x∈[0，

  π

  2

  ]）的最大值為（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：462引用：4難度：0.7

  解析

三、解答題（本題共6題，滿分85分）

• 20．已知函數f（x）=e^x-ax+cosx-2．
  （Ⅰ）求曲線y=f（x）在點（0，f（0））處的切線方程；
  （Ⅱ）若f（x）在（0，+∞）上單調遞增，求實數a的取值范圍；
  （Ⅲ）當a＞1時，判斷f（x）在（0，+∞）零點的個數，并說明理由．
  組卷：171引用：6難度：0.2

  解析

• 21．設數列{a_n}滿足：a₁=1，

  a

  n

  =

  a

  n

  -

  1

  +

  a

  [

  n

  2

  ]

  ，n=2，3，…，其中[x]表示不超過實數x的最大整數．若a_n被正整數p除所得的余數為k,則記a_n=k（modp），若數列中不同的兩項a_i，a_j被p除所得余數相同，則記a_i=a_j（modp）．
  （Ⅰ）直接寫出a₂，a₃，a₄，a₅；
  （Ⅱ）若a_n≡0（mod7），證明：a_2n+1≡a_2n≡a_2n-1（mod7）；
  （Ⅲ）證明：數列{a_n}有無窮多項是7的倍數．
  組卷：30引用：1難度：0.5

  解析