2023-2024學(xué)年天津市和平區(qū)益中學(xué)校高二（上）期中數(shù)學(xué)試卷

一、選擇題（每題3分，共30分）

• 1．橢圓x²+my²=1的焦點(diǎn)在y軸上，長(zhǎng)軸長(zhǎng)是短軸長(zhǎng)的兩倍，則m的值為（　　）

  A． 1 4

  B． 1 2

  C．2

  D．4
  組卷：5378引用：126難度：0.9

  解析

• 2．直線(xiàn)x+a²y+6=0與直線(xiàn)（a-2）x+3ay+2a=0平行，則實(shí)數(shù)a的值為（　　）

  A．3或-1

  B．0或-1

  C．-3或-1

  D．0或3
  組卷：260引用：5難度：0.7

  解析

• 3．過(guò)點(diǎn)A（-

  3

  ，

  2

  ）與點(diǎn)B（-

  2

  ，

  3

  ）的直線(xiàn)的傾斜角為（　　）

  A．45°

  B．135°

  C．45°或135°

  D．60°
  組卷：253引用：11難度：0.8

  解析

• 4．已知直線(xiàn)y=kx與圓x²+（y-2）²=4相交于A，B兩點(diǎn)，若

  |

  AB

  |

  =

  2

  3

  ，則k=（　　）

  A． ± 3 3

  B．±1

  C． ± 3

  D．±2
  組卷：97引用：1難度：0.8

  解析

• 5．若直線(xiàn)y=x+b與曲線(xiàn)y=3-

  4

  x

  -

  x

  2

  有公共點(diǎn)，則b的取值范圍是（　　）

  A．[ 1 - 2 2 ， 1 + 2 2 ]

  B．[ 1 - 2 ，3]

  C．[-1， 1 + 2 2 ]

  D．[ 1 - 2 2 ，3]
  組卷：1909引用：104難度：0.9

  解析

• 6．由直線(xiàn)y=x-1上的一點(diǎn)向圓x²+y²-6x+8=0引切線(xiàn)，則切線(xiàn)長(zhǎng)的最小值為（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：401引用：11難度：0.7

  解析

三、解答題（4道題，共46分）

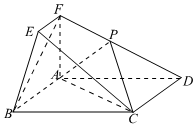• 19．如圖所示的幾何體中，四邊形ABCD為矩形，AF⊥平面ABCD，EF∥AB，AD=2，AB=AF=2EF=1，點(diǎn)P為棱DF的中點(diǎn)．
  （1）求證：BF∥平面APC；
  （2）求直線(xiàn)DE與平面BCF所成角的正弦值；
  （3）求平面ACP與平面BCF的夾角的余弦值．
  組卷：545引用：8難度：0.5

  解析

• 20．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的一個(gè)頂點(diǎn)為（2，0），離心率為

  3

  2

  ，直線(xiàn)y=x+m與橢圓C交于不同的兩點(diǎn)A，B．
  （1）求橢圓C的方程；
  （2）求△OAB面積的最大值，并求此時(shí)直線(xiàn)l的方程．
  組卷：449引用：6難度：0.5

  解析