2022-2023學年福建省福州八中高二(上)適應性數學試卷
發布:2024/8/3 8:0:9
一.選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.若直線ax+y-a+1=0與直線(a-2)x-3y+a=0垂直,則實數a的值為( )
A.-1或3 B.1或-3 C.-1或-3 D.1或3 組卷:290引用:9難度:0.8 -
2.方程x2+y2+2ax-2y+a2+a=0表示圓,則實數a的取值范圍是( )
A.a≤1 B.a<1 C.a>1 D.0<a<1 組卷:558引用:6難度:0.7 -
3.空間四邊形OABC中,
,OA=a,OB=b,且OC=c,OM=23OA,則BN=NC=( )MNA. 12a-23b+12cB. 12a+12b-12cC. -23a+23b+12cD. -23a+12b+12c組卷:282引用:16難度:0.7 -
4.若拋物線x2=12y的焦點與雙曲線
-y2a2=1的一個焦點重合,則此雙曲線的漸近線方程為( )x25A.y=± x52B.y=± x54C.y=± x255D.y=± x45組卷:155引用:6難度:0.7 -
5.設數列{an}前n項和為Sn,已知a1=
,an+1=45,則S2020=( )2an,0≤an≤122an-1,12<an≤1A.1010 B.1012 C.2020 D.2022 組卷:50引用:2難度:0.6 -
6.已知f(x)是周期為2的奇函數,當0<x<1時,f(x)=lgx.設
,a=f(65),b=f(32),則( )c=f(52)A.a<b<c B.b<a<c C.c<b<a D.c<a<b 組卷:965引用:35難度:0.9 -
7.設公差d>0的等差數列{an}的前n項和為Sn,已知a1=5,且a1,a3-1,a6成等比數列,則
的最小值為( )nan-n2SnA. 713B. 25C. 58D.1 組卷:65引用:3難度:0.6
四.解答題:本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
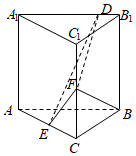 21.已知直三棱柱ABC-A1B1C1中,側面AA1B1B為正方形,AB=BC=2,E,F分別為AC和CC1的中點,D為棱A1B1上的點,BF⊥A1B1.
21.已知直三棱柱ABC-A1B1C1中,側面AA1B1B為正方形,AB=BC=2,E,F分別為AC和CC1的中點,D為棱A1B1上的點,BF⊥A1B1.
(1)證明:BF⊥DE;
(2)當B1D為何值時,面BB1C1C與面DFE所成的二面角的正弦值最小?組卷:9753引用:49難度:0.5 -
22.已知橢圓C:
=1(a>b>0)的左頂點為A,右焦點為F,過點A作斜率為x2a2+y2b2的直線與C相交于A,B,且AB⊥OB,O為坐標原點.33
(1)求橢圓的離心率e;
(2)若b=1,過點F作與直線AB平行的直線l,l與橢圓C相交于P,Q兩點,
(ⅰ)求直線OP的斜率與直線OQ的斜率乘積;
(ⅱ)點M滿足2=OM,直線MQ與橢圓的另一個交點為N,求OP的值.|NM||NQ|組卷:119引用:6難度:0.6


