2023-2024學(xué)年福建省莆田市城廂區(qū)哲理中學(xué)九年級（上）返校考數(shù)學(xué)試卷

一、單選題

• 1．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．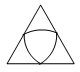

  B．

  C．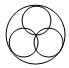

  D．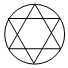
  組卷：93引用：6難度：0.9

  解析

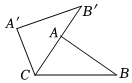• 2．如圖，將△ABC繞點(diǎn)C逆時針旋轉(zhuǎn)一定的角度得到△A′B′C′，此點(diǎn)A在邊B′C上，若BC=5，AC=3，則AB′的長為（　　）

  A．5

  B．4

  C．3

  D．2
  組卷：520引用：10難度：0.6

  解析

• 3．拋物線y=-2（x-2）²-5的頂點(diǎn)坐標(biāo)是（　　）

  A．（-2，5）

  B．（2，5）

  C．（-2，-5）

  D．（2，-5）
  組卷：2890引用：31難度：0.9

  解析

• 4．將二次函數(shù)y=5x²的圖象先向右平移3個單位，再向下平移2個單位，得到的函數(shù)圖象的解析式為（　　）

  A．y=5（x+3）2+2	B．y=5（x-3）2+2
  C．y=5（x+3）2-2	D．y=5（x-3）2-2
  組卷：980引用：14難度：0.7

  解析

• 5．二次函數(shù)y=2x²+3的圖象經(jīng)過（　　）

  A．第一、二象限	B．第三、四象限
  C．第一、三象限	D．第二、四象限
  組卷：1334引用：7難度：0.8

  解析

• 6．廣東春季是流感的高發(fā)時期，某校4月初有一人患了流感，經(jīng)過兩輪傳染后，共25人患流感，假設(shè)每輪傳染中平均每人傳染x人，則可列方程（　　）

  A．1+x+x2=25	B．x+x2=25
  C．（1+x）2=25	D．x+x（1+x）=25
  組卷：1931引用：13難度：0.5

  解析

• 7．如圖，△ABC與△A′B′C′關(guān)于O成中心對稱，下列結(jié)論中不成立的是（　　）

  A．OC=OC′	B．OA=OA′
  C．BC=B′C′	D．∠ABC=∠A′C′B′
  組卷：2911引用：14難度：0.5

  解析

• 8．已知函數(shù)y₁=mx²+n,y₂=nx+m（mn≠0），則兩個函數(shù)在同一坐標(biāo)系中的圖象可能為（　　）

  A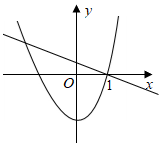．	B．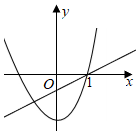
  C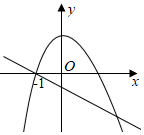．	D．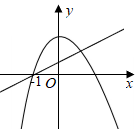
  組卷：2382引用：7難度：0.5

  解析

三、解答題

• 24．如圖，在平面直角坐標(biāo)系xOy中，拋物線L₁：y=x²-2x-3的頂點(diǎn)為P．直線l過點(diǎn)M（0，m）（m≥-3），且平行于x軸，與拋物線L₁交于A、B兩點(diǎn)（B在A的右側(cè)）．將拋物線L₁沿直線l翻折得到拋物線L₂，拋物線L₂交y軸于點(diǎn)C，頂點(diǎn)為D．
  （1）當(dāng)m=1時，求點(diǎn)D的坐標(biāo)；
  （2）連接BC、CD、DB，若△BCD為直角三角形，求此時L₂所對應(yīng)的函數(shù)表達(dá)式；
  （3）在（2）的條件下，若△BCD的面積為3，E、F兩點(diǎn)分別在邊BC、CD上運(yùn)動，且EF=CD，以EF為一邊作正方形EFGH，連接CG，寫出CG長度的最小值，并簡要說明理由．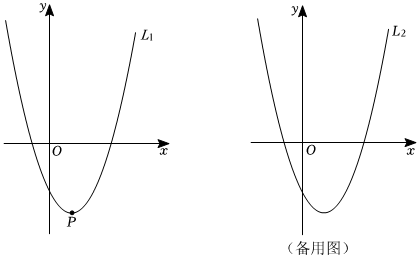
  
  組卷：2802引用：8難度：0.3

  解析

• 25．如圖，等邊△ABC與等腰三角形△EDC有公共頂點(diǎn)C，其中∠EDC=120°，AB=CE=2

  6

  ，連接BE，P為BE的中點(diǎn)，連接PD、AD
  （1）為了研究線段AD與PD的數(shù)量關(guān)系，將圖1中的△EDC繞點(diǎn)C旋轉(zhuǎn)一個適當(dāng)?shù)慕嵌龋笴E與CA重合，如圖2，請直接寫出AD與PD的數(shù)量關(guān)系；
  （2）如圖1，（1）中的結(jié)論是否仍然成立？若成立，請給出證明；若不成立，請說明理由；
  （3）如圖3，若∠ACD=45°，求△PAD的面積．
  
  組卷：1366引用：6難度：0.1

  解析