2023-2024學年廣東省肇慶一中高二（上）期中數學試卷

一、單選題

• 1．對于空間任意兩個非零向量

  a

  ，

  b

  ，

  a

  ∥

  b

  是＜

  a

  ，

  b

  ＞=0的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：72引用：6難度：0.8

  解析

• 2．在棱長為1的正方體ABCD-A₁B₁C₁D₁中，|

  AB

  -

  CB

  +

  C

  B

  1

  |=（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：143引用：9難度：0.8

  解析

• 3．兩條平行直線6x+8y-1=0與6x+8y-9=0間的距離等于（　　）

  A． 1 10

  B． 1 5

  C． 4 5

  D． 4 10
  組卷：52引用：3難度：0.8

  解析

• 4．若直線l的一個方向向量為（-1，

  3

  ），則它的傾斜角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：514引用：28難度：0.8

  解析

• 5．若點P（1，1）在圓

  C

  1

  x

  2

  +

  y

  2

  +

  2

  x

  -

  m

  =

  0

  的外部，則m的取值范圍為（　　）

  A．（-1，4）

  B．（-4，1）

  C．（-1，+∞）

  D．（-∞，4）
  組卷：219引用：8難度：0.7

  解析

• 6．已知向量

  a

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，則向量

  b

  在向量

  a

  上的投影向量為（　　）

  A．（0，-1，-1）

  B．（-1，0，-1）

  C． （ 0 ， 1 2 ， 1 2 ）

  D． （ 1 2 ， 0 ， 1 2 ）
  組卷：211引用：8難度：0.8

  解析

• 7．若圓x²+y²+2x-4y+1=0被直線2ax-by+2=0（a＞0，b＞0）平分，則

  1

  a

  +

  4

  b

  的最小值為（　　）

  A． 1 4

  B． 1 9

  C．4

  D．9
  組卷：74引用：6難度：0.6

  解析

四、解答題

• 21．在平面直角坐標系xOy中，點A的坐標為（1，1），動點P滿足

  |

  PA

  |

  =

  2

  |

  PO

  |

  ．
  （1）求動點P的軌跡C的方程．
  （2）若直線l過點Q（1，2）且與軌跡C相切，求直線l的方程．
  組卷：467引用：11難度：0.5

  解析

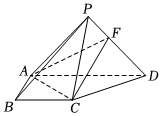• 22．如圖，在四棱錐P-ABCD中，側面PAD⊥底面ABCD，側棱

  PA

  =

  PD

  =

  2

  ，底面ABCD為直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，

  PF

  =

  1

  2

  FD

  ．
  （1）求證：PB∥平面ACF；
  （2）在線段PB上是否存在一點H，使得CH與平面ACF所成角的余弦值為

  30

  6

  ？若存在，求出線段PH的長度；若不存在，請說明理由．
  組卷：201引用：6難度：0.5

  解析