當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省前黃高級中學、常州市溧陽中學高二（上）第一次調研數學試卷

發布：2024/10/28 16:0:2

1．直線
3
x-y-1=0的傾斜角大小（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：301引用：21難度：0.9
解析
2．正項等比數列{a_n}中，a₂=2，a₄=8，則a₁a₇=（　　）
A．4 B．8 C．32 D．64
組卷：308引用：4難度：0.8
解析
3．若拋物線y²=16x上的點M到焦點的距離為12，則它到y軸的距離是（　　）
A．6 B．8 C．9 D．10
組卷：241引用：7難度：0.7
解析
4．過點P（2，1）且被圓C：x²+y²-2x+4y=0截得弦長最長的直線l的方程是（　　）
A．3x-y-5=0 B．3x+y-7=0 C．x-3y+5=0 D．x+3y-5=0
組卷：602引用：16難度：0.9
解析
5．以雙曲線
x
2
4
-
y
2
12
=
1
的焦點為頂點，頂點為焦點的橢圓方程是（　　）
A．
x
2
16
+
y
2
4
=1 B．
x
2
16
+
y
2
8
=1
C．
x
2
12
+
y
2
4
=1 D．
x
2
16
+
y
2
12
=1
組卷：51引用：7難度：0.7
解析
6．在平面直角坐標系中，記d為點P（cosθ，sinθ）到直線x-my-2=0的距離．當θ、m變化時，d的最大值為（　　）
A．1 B．2 C．3 D．4
組卷：6216引用：15難度：0.5
解析
7．已知函數
f
（
x
）
+
f
（
1
x
）
=
2
，若等比數列{a_n}滿足a₁a₂₀₂₁=1，則f（a₁）+f（a₂）+f（a₃）+…+f（a₂₀₂₁）=（　　）
A．
1
2
B．
2021
2
C．2 D．2021
組卷：189引用：4難度：0.8
解析

21．已知拋物線C：x²=2py（p＞0）的焦點為F，點A（2，y₀）在C上，|AF|=2．
（1）求p；
（2）過F作兩條互相垂直的直線l₁，l₂，l₁與C交于M，N兩點，l₂與直線y=-1交于點P，判斷∠PMN+∠PNM是否為定值？若是，求出其值；若不是，說明理由．
組卷：317引用：4難度：0.5
解析
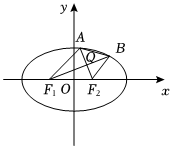22．如圖，已知點F₁，F₂分別是橢圓C：
x
2
4
+
y
2
3
=1的左、右焦點，A，B是橢圓C上不同的兩點，且
F
1
A
=
λ
F
2
B
（λ＞0），連接AF₂，BF₁，設AF₂，BF₁交于點Q．
（1）當λ=2時，求點B的橫坐標；
（2）若△ABQ的面積為
1
2
，試求λ+
1
λ
的值．
組卷：67引用：3難度：0.5
解析

A． x 2 16 + y 2 4 =1	B． x 2 16 + y 2 8 =1
C． x 2 12 + y 2 4 =1	D． x 2 16 + y 2 12 =1

1．直線3x-y-1=0的傾斜角大小（ ）