2022-2023學年北京市海淀區(qū)師達中學九年級（上）第一次段考數(shù)學試卷（10月份）
發(fā)布：2024/4/20 14:35:0
一、選擇題（每題2分，共16分）
-
1．方程2x2-3x-1=0的二次項系數(shù)、一次項系數(shù)、常數(shù)項分別為（ ）
組卷：25引用：2難度：0.8 -
2．拋物線y=（x-1）2+2的頂點坐標為（ ）
組卷：859引用：33難度：0.6 -
3．把拋物線y=
向下平移2個單位，得到拋物線解析式為（ ）12x2組卷：158引用：3難度：0.6 -
4．關(guān)于x的一元二次方程（x-1）2=0的根的情況，下列結(jié)論正確的是（ ）
組卷：58引用：1難度：0.8 -
5．用配方法解一元二次方程x2-4x+1=0時，下列變形正確的是（ ）
組卷：2315引用：57難度：0.6 -
6．生活垃圾無害化處理可以降低垃圾及其衍生物對環(huán)境的影響．據(jù)統(tǒng)計，2017年全國生活垃圾無害化處理能力約為2.5億噸，隨著設施的增加和技術(shù)的發(fā)展，2019年提升到約3.2億噸．如果設這兩年全國生活垃圾無害化處理能力的年平均增長率為x,那么根據(jù)題意可以列方程為（ ）
組卷：455引用：13難度：0.8 -
7．拋物線y=ax2+bx+c上，部分點的橫坐標x與縱坐標y的對應值如表：
則下列結(jié)論正確的有（ ）x …… -1 0 1 2 3 …… y …… 1 -2 -3 -2 1 ……
①a＞0；
②c=-2；
③拋物線的對稱軸為直線x=1；
④方程ax2+bx+c=0的兩個根滿足-1＜x1＜0，2＜x2＜3．組卷：443引用：2難度：0.6 -
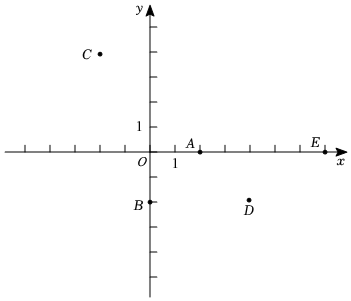8．如圖，在平面直角坐標系中，有五個點，A（2，0），B（0，-2），C（-2，4），D（4，-2），E（7，0）．將二次函數(shù)y=a（x-2）2+m（m≠0）的圖象記為G，下列結(jié)論中正確的有（ ）
①點A一定在G上；
②點B，C，D可以同時在G上；
③點C，E可以同時在G上；
④點C，D，E不可能同時在G上．組卷：110引用：1難度：0.6
二、填空題（每題2分，共16分）
-
9．一元二次方程x2-3x=0的實數(shù)根為 ．
組卷：64引用：2難度：0.6
三、解答題（共68分，17題8分，18題4分，19-21題，23題，25題每題5分，22題，24題，26題，27題每題6分，28題7分）
-
27．在平面直角坐標系xOy中，已知拋物線G：y=ax2-2ax+4（a≠0）．
（1）當a=1時，
①拋物線G的對稱軸為直線x=；
②若拋物線上有兩點（2，y1），（m,y2），且y2＞y1，則m的取值范圍是 ；
（2）已知點A（-1，0），B（4，0），若拋物線G與線段AB恰有一個公共點，結(jié)合圖象，求a的取值范圍．組卷：207引用：4難度：0.7 -
28．在平面直角坐標系xOy中，對于點P（x,y）和Q（x,y′），給出如下定義：
如果y′=，那么稱點Q為點P的“關(guān)聯(lián)點”．y（x≥0）-y（x＜0）
例如點（5，6）的“關(guān)聯(lián)點”為點（5，6），點（-5，6）的“關(guān)聯(lián)點”為點（-5，-6）．
（1）在點E（0，0），F(xiàn)（2，5），G（-1，-1），H（-3，5）中，的“關(guān)聯(lián)點”在函數(shù)y=2x+1的圖象上；
（2）如果一次函數(shù)y=x+3圖象上點M的“關(guān)聯(lián)點”是N（m,2），求點M的坐標；
（3）如果點P在函數(shù)y=-x2+4（-2＜x≤a）的圖象上，其“關(guān)聯(lián)點”Q的縱坐標y′的取值范圍是-4＜y′≤4，求實數(shù)a的取值范圍．
組卷：699引用：8難度：0.6